We introduce price freeze options into a model of sequential search. The model's predictions are tested in a laboratory experiment. The experiment varies (1) whether freezing is possible or not, (2) the cost of freezing, and (3) the time horizon. Overall, the observed treatment effects are consistent with the predictions of our model. Assuming that individuals experience regret, fail to ignore sunk search costs, misperceive the number of periods remaining, or are risk-averse, does not improve upon the performance of the model. Our results support the use of the assumption of optimal search behavior in theoretical and empirical studies.

We construct asset markets that are similar to those studied by Smith, Suchanek and Williams (Econometrica. 56, 1119-1151) in which bubbles and crashes tended to occur. The main difference between the markets studied here and those studied by Smith et al. is that in the markets studied here, the fundamental value of the asset is constant over the entire life of the asset. In four of the eight sessions reported here, we observe bubbles, which are prices considerably higher than fundamental values. The data suggest that the frequent payment of dividends is a major cause of bubble formation. The property that the fundamental value remains constant over the course of the trading horizon is not sufficient to eliminate the possibility of a bubble.

We investigate experimentally how granting a manager stock ownership and the opportunity to trade shares of a company’s stock influence the manager’s effort and the overall behavior of the market for the company’s shares. In our design, managerial effort affects the fundamental value of the firm. Our findings suggest that endowing a manager with stock does not significantly increase the manager’s effort. When the manager is allowed to trade the company’s shares, however, she tends to accumulate additional shares, increase her effort, and raise company value. In all of our treatments, prices tend to reflect underlying fundamentals, and bubbles are rare.

We use time, rather than money, as the salient component of subjects’ incentives in three workhorse experimental paradigms. The use of waiting time can be interpreted as a special type of real effort condition, in which it is particularly straightforward to achieve experimental control over incentives. The three experiments, commonly employed to study social preferences, are the dictator game, the ultimatum game and the trust game. All subjects in a session earn the same participation fee, but their choices affect the time at which they are permitted to leave the laboratory. Decisions that are associated with greater own payoff translate into the right to depart earlier. The modal proposal in both the dictator and ultimatum games is an equal split of the waiting time. In the trust game, there is substantial trust and reciprocity. Overall, social preferences are evident in time allocation decisions. We compare subjects’ decisions over time and money and find no significant differences in average decisions. The pattern of results suggests that results obtained in the laboratory with money as the medium of reward generalize to other reward media.

In this paper we propose and test a contracting mechanism, Multi-Contract Cost Sharing (MCCS), for use in the management of a sequence of projects. The mechanism is intended for situations where (1) the contractor knows more about the true costs of various projects than does the contracting agency (adverse selection), and (2) unobservable effort on the part of the contractor may lead to cost reductions (moral hazard). The proposed process is evaluated in an experimental environment that includes the essential economic features of the NASA process for the acquisition of Space Science Strategic missions. The environment is complex and the optimal mechanism is unknown. The design of the MCCS mechanism is based on the optimal contract for a simpler related environment. We compare the performance of the proposed process to theoretical benchmarks and to an implementation of the current NASA ‘cost cap’ procurement process. The data indicate that the proposed MCCS process generates significantly higher value per dollar spent than using cost caps, because it allocates resources more efficiently among projects and provides greater incentives to engage in cost-reducing innovations.

Conditional cooperation is the tendency to cooperate if and only if others do so as well. It is the most common behavior in social dilemmas. We study how the incidence of conditional cooperation in the public goods game, the most widely studied social dilemma in experimental economics, varies with group size. In a laboratory experiment, we apply the strategy method to elicit how participants’ willingness to contribute to a public good depends on other group members’ decisions. A within-subject design allows us to evaluate and compare an individual participant's contribution behavior in different-sized groups. Two main findings emerge. First, the share of players who are conditional cooperators is consistent across group sizes. Second, the strategies chosen imply that conditional cooperators hold a (correct) belief that others are more cooperative in a larger than in a smaller group.

The replication crisis across several disciplines raises challenges for behavioural sciences in general. In this report, we review the lessons for experimental economists of these developments. We present the new research methods and practices which are being proposed to improve the replicability of scientific studies. We discuss how these methods and practices can have a positive impact in experimental economics and the extent to which they should be encouraged.

As in other sciences, an economic experiment is an artificial situation created by a researcher for the purpose of answering one or more scientific questions. Experiments of various types are used in economics to understand the causes of poverty and how it might be alleviated. The methods can identify causal relationships between variables and thereby isolate factors that can lead to poverty as well as to document the behavioral consequences of poverty. Experiments can also be used to provide test beds for proposed policies to alleviate poverty. This essay describes a variety of ways in which experiments have been employed to understand and combat poverty. A line of laboratory experiments that considers which economic institutions are conducive to economic growth is discussed in detail. The results show that decentralized markets are conducive to allowing an economy to operate as efficiently as it can. However, in an economy with a theoretical “poverty trap,” the market works more efficiently if accompanied by a democratic voting process and freedom of communication.

We study whether probability weighting is observed when individuals are presented with a series of choices between lotteries consisting of real non-monetary adverse outcomes, electric shocks. Our estimation of the parameters of the probability weighting function proposed by Tversky and Kahneman (1992) are similar to those obtained in previous studies of lottery choice for negative monetary payoffs and negative hypothetical payoffs. In addition, common ratio violations in choice behavior are widespread. Our results provide evidence that probability weighting is a general phenomenon, independent of the source of disutility.

We investigate the relationship between traders’ expectations and market outcomes with experimental asset market data. The data show that those who have high price expectations buy more frequently and submit higher bids, and those who hold low price expectations sell more frequently and submit lower bids. Traders who have more accurate expectations achieve greater earnings. Simulations using only belief data reproduce the pricing patterns observed in the market well, indicating that the heterogeneity of expectations is a key to explaining market activity.

Existence theorems and asymptotic properties will be obtained for boundary value problems of the form in an unbounded domain Ω⊆ RN(N ≥3) with smooth boundary, where Δ denotes the TV-dimensional Laplacian, τ — (N+ 2)/ (N — 2) is the critical Sobolev exponent, and is the completion of in the L2(Ω) norm of .

An existence theorem is obtained for a fourth-order semilinear elliptic problem in RN involving the critical Sobolev exponent (N + 4)/(N − 4), N>4. A preliminary result is that the best constant in the Sobolev embedding L2N/(N–4) (RN) is attained by all translations and dilations of (1 + ∣x∣2)(4-N)/2. The best constant is found to be

A class of weakly coupled systems of semilinear elliptic partial differential equations is considered in an exterior domain in ℝN, N > 3. Necessary and sufficient conditions are given for the existence of a positive solution (componentwise) with the asymptotic decay u(x) = O(|x|2-N ) as |x| —> ∞. Additional results concern the existence and structure of positive solutions u with finite energy in a neighbourhood of infinity.

Semilinear elliptic partial differential systems of second order with weak coupling are considered in exterior domains Ω ⊆ ℝN, N≧3. Conditions on the nonlinearities are given which guarantee the existence of solutions u with positive components in Ω such that u|∂Ω = 0 and u(x)→0 uniformly as |x|→∞. Asymptotic decay estimates for the solutions are established, including an exponential decay law under extra hypotheses.

Our main objective is to prove the existence of a pair of positive, exponentially decaying, classical solutions of the semilinear elliptic eigenvalue problem

1.1

in a smooth unbounded domain Ω ⊂ R N, N ≧ 2, where λ is a positive parameter and L is a uniformly elliptic operator in Ω defined by

The semilinear elliptic boundary value problem

1.1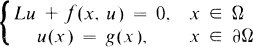

will be considered in an exterior domain Ω ⊂ R n , n ≥ 2, with boundary ∂Ω ∊ C 2 + α , 0 < α < 1, where

1.2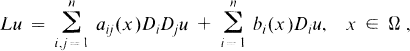

D i = ∂/∂x i , i = 1, …, n. The coefficients aij , bi in (1.2) are assumed to be real-valued functions defined in Ω ∪ ∂Ω such that each 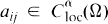, , 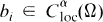and (aij (x)) is uniformly positive definite in every bounded domain in Ω. The Hölder exponent α is understood to be fixed throughout, 0 < α < 1 . The regularity hypotheses on f and g are stated as H 1 near the beginning of Section 2.