We analyse a Markovian SIR epidemic model where individuals either recover naturally or are diagnosed, leading to isolation and potential contact tracing. Our focus is on digital contact tracing via a tracing app, considering both its standalone use and its combination with manual tracing. We prove that as the population size n grows large, the epidemic process converges to a limiting process, which, unlike with typical epidemic models, is not a branching process due to dependencies created by contact tracing. However, by grouping to-be-traced individuals into macro-individuals, we derive a multi-type branching process interpretation, allowing computation of the reproduction number R. This is then converted to an individual reproduction number 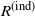$R^\mathrm{(ind)}$, which, in contrast to R, decays monotonically with the fraction of app-users, while both share the same threshold at 1. Finally, we compare digital (only) contact tracing and manual (only) contact tracing, proving that the critical fraction of app-users, 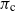$\pi_{\mathrm{c}}$, required for 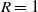$R=1$ is higher than the critical fraction manually contact-traced, 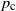$p_{\mathrm{c}}$, for manual tracing.

Suppose that X and Y are two real normed spaces. A map $f:X\rightarrow Y$ is called a min-phase-isometry if it satisfies

$$ \begin{align*} \min\{\|f(x)+f(y)\|,\|f(x)-f(y)\|\}=\min\{\|x+y\|,\|x-y\|\} \quad (x,y\in X). \end{align*} $$

We present properties of min-phase-isometries in the case that Y is strictly convex and show that if a min-phase-isometry f (not necessarily surjective) fixes the origin, then it is phase-equivalent to a linear isometry, that is, $f(x)=\varepsilon (x)g(x)$ for $x\in X$, where $g:X\rightarrow Y$ is a linear isometry and $\varepsilon $ is a map from X to $\{-1,1\}$.

Low urinary iodine concentration (UIC) is associated with dyslipidaemia in adults but is not well characterised in adolescents. Because dyslipidaemia is a cardiovascular risk factor, identifying such an association in adolescents would allow for the prescription of appropriate measures to maintain cardiovascular health. The present study addresses this question using data in the 2001–2012 National Health and Nutrition Examination Survey for 1692 adolescents aged 12–19 years. Primary outcomes were UIC, cardiometabolic risk factors and dyslipidaemia. Data for subjects categorised by low and normal UIC and by sex were analysed by univariate and multivariate logistic regression. Treating UIC as the independent variable, physical activity level, apoB and lipid profiles differed significantly between subjects with low and normal UIC. Subjects with low UIC had a significantly greater risk of elevated total cholesterol (TC) (95 % CI 1·37, 2·81), elevated non-HDL (95 % CI 1·33, 2·76) and elevated LDL (95 % CI 1·83, 4·19) compared with those with normal UIC. Treating UIC as a dependent variable, the risk of low UIC was significantly greater in those with higher apoB (95 % CI 1·52, 19·08), elevated TC (≥4·4mmol/l) (95 % CI 1·37, 2·81) and elevated non-HDL (≥3·11mmol/l) (95 % CI 1·33, 2·76) than in those with normal UIC. These results show that male and female adolescents with low UIC tend to be at greater risk of dyslipidaemia and abnormal cardiometabolic biomarkers, though the specific abnormal parameters differed between sexes. These results may help to identify youth who would benefit from interventions to improve their cardiometabolic risk.