In aerodynamic and hydrodynamic devices and locomotive organisms, passive appendages have practical purposes such as drag reduction and flow control. Although these appendages also affect the dynamics of freely falling bodies, underlying principles of their functions remain elusive. We investigate experimentally the dynamics of a falling sphere with a filament appended on its rear side by varying the ratio of filament length to sphere diameter (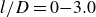$l/D=0{-}3.0$) and sphere-to-fluid density ratio (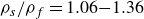$\rho _s/\rho _f= 1.06{-}1.36$), and maintaining a similar dimensionless moment of inertia (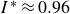$I^* \approx 0.96$). At the Reynolds number of 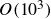$O(10^3)$, a sphere without any filament exhibits vertical descent. However, the falling of the sphere with a filament is accompanied by periodic horizontal displacements, and the degree of zigzag motion is maximised under specific filament length. The filament induces periodic rotation of the sphere by shifting the centre of mass of the entire model and through the hydrodynamic interaction of the filament with the surrounding fluid. The rotation of the sphere increases the drag force acting on the model, reducing tangential velocity along the trajectory by 14 % compared to a plain sphere. Furthermore, the sphere rotation enhances the lift force normal to the trajectory, extending trajectory length by 5 %. These combined effects improve falling time over a certain vertical distance by 20 % compared to the plain sphere. With increasing sphere density, the effects of the filament on the falling dynamics weaken, because the offset distance between the centre of mass of the model and the geometric centre of the sphere becomes smaller.

Water stuck in the ear is a common problem during showering, swimming or other water activities. Having water trapped in the ear canal for a long time can lead to ear infections and possibly result in hearing loss. A common strategy for emptying water from the ear canal is to shake the head, where high acceleration helps remove the water. In this present study, we rationalize the underlying mechanism of water ejection/removal from the ear canal by performing experiments and developing a stability theory. From the experiments, we measure the critical acceleration to remove the trapped water inside different sizes of canals. Our theoretical model, modified from the Rayleigh–Taylor instability, can explain the critical acceleration observed in experiments, which strongly depends on the radius of the ear canal. The resulting critical acceleration tends to increase, especially in smaller ear canals, which indicates that shaking heads for water removal can be more laborious and potentially threatening to children due to their small size of the ear canal compared with adults.

The impact of a drop train, a series of identical liquid drops separated by a constant distance, on a liquid pool initially generates a long slender cavity. However, the cavity soon collapses and turns into a shallow funnel. Here we theoretically model the dynamic profile of the elongated cavity and the steady shape of the funnel, which are then shown to agree well with experiment. When the liquid inertia plays a dominant role, the cavity assumes a parabolic profile that depends only on the drop diameter and the centre-to-centre spacing of adjacent drops. We consider the capillary forces as well as the drop impact force to obtain the shape of the funnel that persists once the elongated cavity collapses. Our study allows for predicting the interfacial morphology by the impact of a drop train and designing impact conditions useful for semiconductor cleaning processes.

Liquid films on wettable solid surfaces can be disturbed to dewet when low surface tension liquids or surfactants are added because the surface tension difference gives rise to stresses on the film interface. Here we consider an alcohol drop placed above a thin aqueous film, which punctures a hole in the film starting from underneath the alcohol drop. Such film dewetting is attributed to the Marangoni effects caused by the spatial gradient of alcohol vapour concentration. We measure the liquid–gas interfacial tension of aqueous liquids rapidly responding to the surrounding isopropyl alcohol vapour concentration, and observe evolution of the film morphology consisting of central hole, fringe film, thinning region and bulk. We construct scaling laws to predict the dewetting rates of the film by considering the Marangoni stress, viscous shear stress and evaporation. It is shown that our experiments are consistent with our theory.

Population growth has been evoked both as a causal factor and consequence of the transition to agriculture. The use of radiocarbon (14C) dates as proxies for population allows for reevaluations of population as a variable in the transition to agriculture. In Korea, numerous rescue excavations during recent decades have offered a wealth of 14C data for this application. A summed probability distribution (SPD) of 14C dates is investigated to reconstruct population trends preceding and following adoptions of food production in prehistoric Korea. Important cultivars were introduced to Korea in two episodes: millets during the Chulmun Period (ca. 6000–1500 BCE) and rice during the Mumun Period (ca. 1500–300 BCE). The SPD suggests that while millet production had little impact on Chulmun populations, a prominent surge in population appears to have followed the introduction of rice. The case in prehistoric Korea demonstrates that the adoption of food production does not lead inevitably towards sustained population growth. Furthermore, the data suggest that the transition towards intensive agriculture need not occur under conditions of population pressure resulting from population growth. Rather, intensive rice farming in prehistoric Korea began during a period of population stagnation.

A few epidemiological data are available assessing the associations of intakes of sodium (Na) and potassium (K) with non-alcoholic fatty liver disease (NAFLD). We aimed to examine the associations of dietary intake of Na and K with the prevalence of ultrasound-diagnosed NAFLD. We performed a cross-sectional study of 100 177 participants (46 596 men and 53 581 women) who underwent a health screening examination and completed a FFQ at the Kangbuk Samsung Hospital Total Healthcare Centers, South Korea, between 2011 and 2013. NAFLD was defined by ultrasonographic detection of fatty liver in the absence of excessive alcohol intake or other known causes of liver disease. The proportion of NAFLD was 35·6 % for men and 9·8 % for women. Increasing prevalence of NAFLD was observed with increasing Na intake. The multivariable-adjusted prevalence ratios (PR) of NAFLD comparing the highest with the lowest quintile of energy-adjusted Na intake were 1·25 (95 % CI 1·18, 1·32; P trend<0·001) in men and 1·32 (95 % CI 1·18, 1·47; P trend <0·001) in women. However, when we additionally adjusted for body fat percentage, the association became attenuated; the corresponding PR of NAFLD were 1·15 (95 % CI 1·09, 1·21) in men and 1·06 (95 % CI 0·95, 1·17) in women. No inverse association was observed for energy-adjusted K intake. Our findings suggest that higher Na intake is associated with a greater prevalence of NAFLD in young and middle-aged asymptomatic adults, which might be partly mediated by adiposity.

Extreme wetting properties of solids, either superhydrophobic or superhydrophilic, provide versatile methods to achieve unusual liquid deposit morphologies, such as liquid pearls or polygonal films. Here we report the dynamics of liquid drops that impact on solid surfaces where the extreme wetting properties are coupled in such a way that a superhydrophilic annulus is patterned on a superhydrophobic background. The drop that initially spreads on the inner superhydrophobic region is arrested by the hydrophilic annulus. The liquid deposit gets destabilized because of the strong water repellence of the inner region, exhibiting the burst and disengagement of the liquid film. This process leads to the formation of a liquid ring defined by the annulus pattern, which has practical implications in rapid printing of functional liquids. We visualize such drop dynamics with a high-speed camera and characterize their salient features by combining experimental measurements and theoretical considerations.