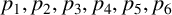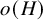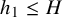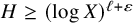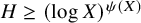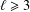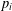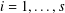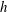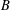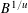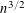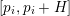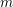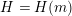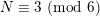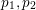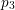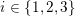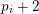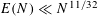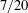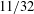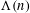Refine search
Actions for selected content:
34 results
DIGITALLY RESTRICTED SETS AND THE GOLDBACH CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 04 February 2025, pp. 469-477
- Print publication:
- June 2025
-
- Article
- Export citation
ON AN AVERAGE GOLDBACH REPRESENTATION FORMULA OF FUJII
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 17 January 2023, pp. 511-532
- Print publication:
- June 2023
-
- Article
- Export citation
A PAIR OF EQUATIONS IN EIGHT PRIME CUBES AND POWERS OF 2
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 14 December 2022, pp. 244-253
- Print publication:
- October 2023
-
- Article
- Export citation
ON THE WARING–GOLDBACH PROBLEM FOR ONE SQUARE, FOUR CUBES AND ONE BIQUADRATE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 15 September 2022, pp. 416-431
- Print publication:
- June 2023
-
- Article
- Export citation
On the Hardy–Littlewood–Chowla conjecture on average
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 27 July 2022, e57
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN EXPLICIT VERSION OF CHEN’S THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 344-346
- Print publication:
- April 2022
-
- Article
-
- You have access
- HTML
- Export citation
DISTRIBUTION OF INTEGERS WITH PRESCRIBED STRUCTURE AND APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 19 October 2020, pp. 509-511
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
ON SOME QUESTIONS OF PARTITIO NUMERORUM: TRES CUBI
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 21 April 2020, pp. 223-244
- Print publication:
- January 2021
-
- Article
- Export citation
ON SUMS OF TWO PRIME SQUARES, FOUR PRIME CUBES AND POWERS OF TWO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 207-216
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Vinogradov’s three primes theorem with primes having given primitive roots
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 05 November 2019, pp. 75-110
- Print publication:
- January 2021
-
- Article
- Export citation
SHORT INTERVALS ASYMPTOTIC FORMULAE FOR BINARY PROBLEMS WITH PRIME POWERS, II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 08 April 2019, pp. 351-370
- Print publication:
- December 2020
-
- Article
- Export citation
Zeroes of Polynomials With Prime Inputs and Schmidt’s
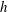 $h$-invariant
$h$-invariant
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 07 February 2019, pp. 805-833
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
PRIME SOLUTIONS TO POLYNOMIAL EQUATIONS IN MANY VARIABLES AND DIFFERING DEGREES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 18 October 2018, e19
-
- Article
-
- You have access
- Open access
- Export citation
SARNAK’S SATURATION PROBLEM FOR COMPLETE INTERSECTIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 1 / 2019
- Published online by Cambridge University Press:
- 24 August 2018, pp. 1-56
- Print publication:
- 2019
-
- Article
- Export citation
GOLDBACH REPRESENTATIONS IN ARITHMETIC PROGRESSIONS AND ZEROS OF DIRICHLET L-FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 1 / 2019
- Published online by Cambridge University Press:
- 24 August 2018, pp. 57-97
- Print publication:
- 2019
-
- Article
- Export citation
THE GOLDBACH PROBLEM FOR PRIMES THAT ARE SUMS OF TWO SQUARES PLUS ONE
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 25 January 2018, pp. 20-70
- Print publication:
- 2018
-
- Article
- Export citation
Vinogradov’s three primes theorem with almost twin primes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 6 / June 2017
- Published online by Cambridge University Press:
- 20 April 2017, pp. 1220-1256
- Print publication:
- June 2017
-
- Article
- Export citation
ON PAIRS OF GOLDBACH–LINNIK EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 199-208
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
ON SUMS OF FOUR SQUARES OF PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 348-361
- Print publication:
- 2016
-
- Article
- Export citation
EXPONENTIAL SUMS OVER PRIMES IN SHORT INTERVALS AND AN APPLICATION TO THE WARING–GOLDBACH PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 508-523
- Print publication:
- 2016
-
- Article
- Export citation