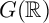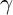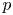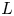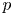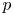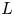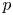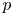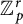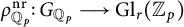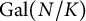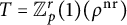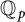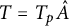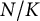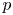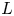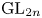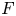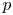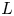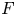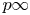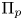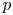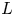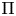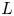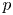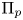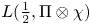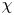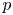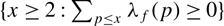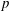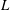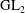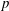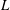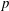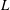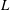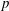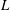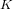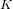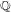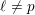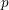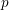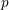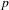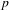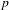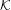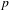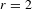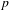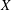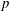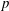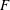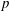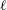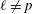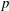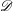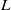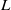Refine search
Actions for selected content:
15 results
ON THE CONVERGENCE OF ZETA FUNCTIONS OF PREHOMOGENEOUS VECTOR SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 311-356
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The error term in the truncated Perron formula for the logarithm of an L-function
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 09 March 2023, pp. 1122-1134
- Print publication:
- December 2023
-
- Article
- Export citation
GENERALIZED ZETA INTEGRALS ON CERTAIN REAL PREHOMOGENEOUS VECTOR SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 50-87
- Print publication:
- March 2023
-
- Article
- Export citation
Sum expressions for Kubota–Leopoldt $p$
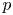 -adic $L$
-adic $L$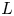 -functions
-functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. 460-479
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The epsilon constant conjecture for higher dimensional unramified twists of
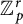 ${\mathbb Z}_p^r$(1)
${\mathbb Z}_p^r$(1)
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 1405-1449
- Print publication:
- October 2022
-
- Article
- Export citation
L-functions of GL2n: p-adic properties and non-vanishing of twists
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 08 January 2021, pp. 2437-2468
- Print publication:
- December 2020
-
- Article
- Export citation
IGUSA’S CONJECTURE FOR EXPONENTIAL SUMS: OPTIMAL ESTIMATES FOR NONRATIONAL SINGULARITIES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 7 / 2019
- Published online by Cambridge University Press:
- 31 July 2019, e3
-
- Article
-
- You have access
- Open access
- Export citation
Chebyshev’s bias for analytic L-functions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 22 March 2019, pp. 103-140
- Print publication:
- July 2020
-
- Article
- Export citation
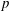 $p$-adic
$p$-adic 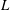 $L$-functions for
$L$-functions for 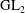 $\text{GL}_{2}$
$\text{GL}_{2}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1019-1059
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
An application of the
 $p$ -adic analytic class number formula
$p$ -adic analytic class number formula
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 June 2016, pp. 217-228
-
- Article
-
- You have access
- Export citation
Compatibility of arithmetic and algebraic local constants (the case
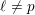 $\ell \neq p$)
$\ell \neq p$)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 9 / September 2015
- Published online by Cambridge University Press:
- 08 April 2015, pp. 1626-1646
- Print publication:
- September 2015
-
- Article
- Export citation
 $p$-ADIC EISENSTEIN SERIES AND
$p$-ADIC EISENSTEIN SERIES AND  $L$-FUNCTIONS OF CERTAIN CUSP FORMS ON DEFINITE UNITARY GROUPS
$L$-FUNCTIONS OF CERTAIN CUSP FORMS ON DEFINITE UNITARY GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 21 November 2014, pp. 471-510
- Print publication:
- July 2016
-
- Article
- Export citation
Product formula for p -adic epsilon factors
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 08 May 2014, pp. 275-377
- Print publication:
- April 2015
-
- Article
- Export citation
On the gcd of local Rankin–Selberg integrals for even orthogonal groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 20 December 2012, pp. 587-636
- Print publication:
- April 2013
-
- Article
- Export citation
p-units in ray class fields of real quadratic number fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 364-392
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation