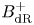 ${B^+_{{\rm dR}}}$-Grassmannian
${B^+_{{\rm dR}}}$-Grassmannian
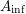 $A_{\text{inf}}$-cohomology in the semistable case
$A_{\text{inf}}$-cohomology in the semistable case
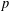 $p$ -ADIQUE
$p$ -ADIQUE
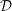 ${\mathcal{D}}$-conjecture
${\mathcal{D}}$-conjecture
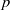 $p$-ADIC HODGE THEORY FOR RIGID-ANALYTIC VARIETIES
$p$-ADIC HODGE THEORY FOR RIGID-ANALYTIC VARIETIES