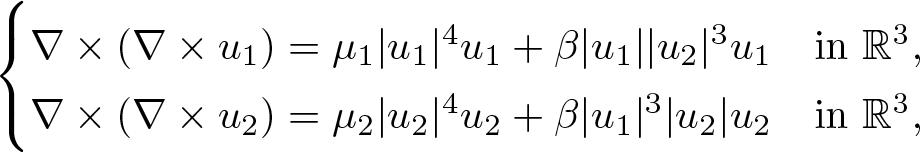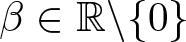Refine search
Actions for selected content:
14 results
Ground state solution for weakly coupled time-harmonic Maxwell’s equations with critical exponent
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 July 2025, pp. 1-31
-
- Article
- Export citation
Unique compact representation of magnetic fields using truncated solid harmonic expansions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 1012-1039
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SYMMETRY RESTORATION IN COLLISIONS OF SOLITONS IN FRACTIONAL COUPLERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 03 December 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Edge corrections for parallel-plate capacitors
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 30 April 2020, pp. 226-241
-
- Article
-
- You have access
- Open access
- Export citation
Standing waves of modified Schrödinger equations coupled with the Chern–Simons gauge theory
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 12 March 2019, pp. 1915-1936
- Print publication:
- August 2020
-
- Article
- Export citation
Spectral transitions for Aharonov-Bohm Laplacians on conical layers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 26 January 2019, pp. 1663-1687
- Print publication:
- December 2019
-
- Article
- Export citation
RECIPROCITY RELATIONS FOR A CONDUCTIVE SCATTERER WITH A CHIRAL CORE IN QUASI-STATIC FORM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 60 / Issue 1 / July 2018
- Published online by Cambridge University Press:
- 03 July 2018, pp. 86-94
-
- Article
-
- You have access
- Export citation
Pinning Effect on Current-Induced Domain Wall Motion in Nanostrip
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 837-851
- Print publication:
- November 2017
-
- Article
- Export citation
Existence of travelling-wave solutions representing domain wall motion in a thin ferromagnetic nanowire
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 395-407
- Print publication:
- April 2018
-
- Article
- Export citation
On the Magneto-Heat Coupling Model for Large Power Transformers
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 06 July 2017, pp. 683-711
- Print publication:
- September 2017
-
- Article
- Export citation
On isotropic cloaking and interior transmission eigenvalue problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 22 May 2017, pp. 253-280
-
- Article
- Export citation
An almost-periodic solution of Hasegawa–Wakatani equations with vanishing resistivity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 23 June 2016, pp. 983-1003
- Print publication:
- October 2016
-
- Article
- Export citation
Fully Discrete A-ø Finite Element Method forMaxwell’s Equations with a Nonlinear Boundary Condition
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 8 / Issue 4 / November 2015
- Published online by Cambridge University Press:
- 10 November 2015, pp. 605-633
- Print publication:
- November 2015
-
- Article
- Export citation
Landau-Lifshitz equation of ferromagnetism with external magnetic field
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 299-316
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation