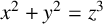 $x^2+y^2=z^3$
$x^2+y^2=z^3$
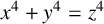 $x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF
$x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF 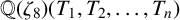 ${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
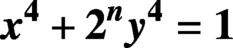 $\boldsymbol{x}^{\boldsymbol{4}} \boldsymbol{+} \boldsymbol{2}^{\boldsymbol{n}}\boldsymbol{y}^{\boldsymbol{4}} \boldsymbol{=} \boldsymbol{1}$ IN QUADRATIC NUMBER FIELDS
$\boldsymbol{x}^{\boldsymbol{4}} \boldsymbol{+} \boldsymbol{2}^{\boldsymbol{n}}\boldsymbol{y}^{\boldsymbol{4}} \boldsymbol{=} \boldsymbol{1}$ IN QUADRATIC NUMBER FIELDS