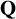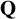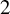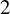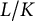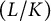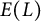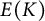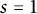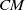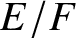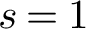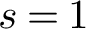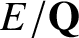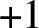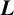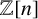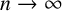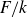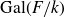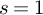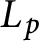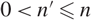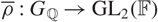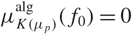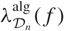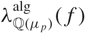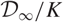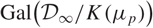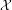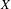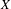Refine search
Actions for selected content:
70 results
On the Fitting ideals of anticyclotomic Selmer groups of elliptic curves with good ordinary reduction
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 14 July 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On L-values of elliptic curves twisted by cubic Dirichlet characters
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Class groups and Selmer groups in special families
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 10 June 2025, pp. 1315-1337
- Print publication:
- December 2025
-
- Article
- Export citation
Congruent elliptic curves and the
 $\tau $-component in the Iwasawa main conjecture
$\tau $-component in the Iwasawa main conjecture
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 29 May 2025, pp. 373-408
- Print publication:
- September 2025
-
- Article
- Export citation
Complete verification of strong BSD for many modular abelian surfaces over
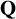 ${\mathbf {Q}}$
${\mathbf {Q}}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 January 2025, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal subfields of elliptic curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1029-1045
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kato’s main conjecture for potentially ordinary primes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 26 January 2024, pp. 338-358
- Print publication:
- May 2024
-
- Article
- Export citation
ON THE FIBRES OF AN ELLIPTIC SURFACE WHERE THE RANK DOES NOT JUMP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 12 December 2022, pp. 276-282
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SPECIAL VALUES OF ZETA-FUNCTIONS OF REGULAR SCHEMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 06 December 2022, pp. 495-519
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chow groups and L-derivatives of automorphic motives for unitary groups, II.
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 04 March 2022, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
VALUES OF ZETA FUNCTIONS OF ARITHMETIC SURFACES AT
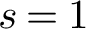 $s=1$
$s=1$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 28 February 2022, pp. 2455-2496
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INDIVISIBILITY OF HEEGNER CYCLES OVER SHIMURA CURVES AND SELMER GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 2297-2336
- Print publication:
- September 2023
-
- Article
- Export citation
On the nonvanishing of generalised Kato classes for elliptic curves of rank 2
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 February 2022, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE p-ADIC GROSS–ZAGIER FORMULA ON SHIMURA CURVES, II: NONSPLIT PRIMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 2199-2240
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
APÉRY LIMITS FOR ELLIPTIC
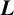 $\boldsymbol {L}$-VALUES
$\boldsymbol {L}$-VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 19 January 2022, pp. 273-279
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Congruences for critical values of higher derivatives of twisted Hasse–Weil L-functions, III
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 19 October 2021, pp. 431-456
- Print publication:
- September 2022
-
- Article
- Export citation
SPECIAL VALUES OF THE ZETA FUNCTION OF AN ARITHMETIC SURFACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 15 March 2021, pp. 2043-2091
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation
Bounding Selmer Groups for the Rankin–Selberg Convolution of Coleman Families
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 17 July 2020, pp. 805-853
- Print publication:
- June 2021
-
- Article
- Export citation
Variation of the algebraic λ-invariant over a solvable extension
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 21 November 2019, pp. 499-521
- Print publication:
- May 2021
-
- Article
- Export citation
TATE’S CONJECTURE AND THE TATE–SHAFAREVICH GROUP OVER GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 17 September 2019, pp. 1001-1022
- Print publication:
- May 2021
-
- Article
- Export citation