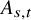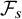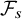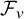Refine search
Actions for selected content:
93 results
Intrinsic stochastic differential equations and the extended Itô formula on manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 12 December 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stochastic Volterra integral equations with ranks as scaling limits of parallel infinite-server queues under weighted shortest queue policy
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 02 December 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Well-posedness and averaging principle for non-Gaussian McKean–Vlasov stochastic differential equations with locally Lipschitz coefficients
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-44
-
- Article
- Export citation
STOCHASTIC MODELLING OF WILDFIRE SPREAD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 28 July 2025, pp. 399-400
- Print publication:
- October 2025
-
- Article
-
- You have access
- HTML
- Export citation
Limit theorems of stochastic differential equations with jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1429-1445
- Print publication:
- December 2025
-
- Article
- Export citation
Averaging principle for the fast–slow McKean–Vlasov stochastic differential equations driven by mixed fractional Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 05 June 2025, pp. 1260-1279
- Print publication:
- December 2025
-
- Article
- Export citation
Approximation of the invariant measure for stable stochastic differential equations by the Euler–Maruyama scheme with decreasing step sizes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 31 March 2025, pp. 1000-1030
- Print publication:
- September 2025
-
- Article
- Export citation
Asymptotic expansion of the invariant measure for Markov-modulated ODEs at high frequency
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 30 January 2025, pp. 898-924
- Print publication:
- September 2025
-
- Article
- Export citation
Pullback measure attractors for non-autonomous stochastic lattice systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-20
-
- Article
- Export citation
Error bounds for one-dimensional constrained Langevin approximations for nearly density-dependent Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 26 July 2024, pp. 825-867
- Print publication:
- September 2024
-
- Article
- Export citation
Change of measure in a Heston–Hawkes stochastic volatility model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 24 July 2024, pp. 1370-1399
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An extension of the stochastic sewing lemma and applications to fractional stochastic calculus
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 April 2024, e52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Skew Ornstein–Uhlenbeck processes with sticky reflection and their applications to bond pricing
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1172-1195
- Print publication:
- December 2024
-
- Article
- Export citation
Invariant measures and large deviation principles for stochastic Schrödinger delay lattice systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1813-1854
- Print publication:
- October 2025
-
- Article
- Export citation
Continuous dependence of stationary distributions on parameters for stochastic predator–prey models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 February 2024, pp. 1010-1028
- Print publication:
- September 2024
-
- Article
- Export citation
An exponential nonuniform Berry–Esseen bound of the maximum likelihood estimator in a Jacobi process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 14 February 2024, pp. 909-926
- Print publication:
- September 2024
-
- Article
- Export citation
ON MODELLING WATER QUALITY WITH STOCHASTIC DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 09 January 2024, pp. 273-284
-
- Article
-
- You have access
- HTML
- Export citation
Speed of extinction for continuous-state branching processes in a weakly subcritical Lévy environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 886-908
- Print publication:
- September 2024
-
- Article
- Export citation
Stochastic differential equation approximations of generative adversarial network training and its long-run behavior
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 465-489
- Print publication:
- June 2024
-
- Article
- Export citation
SUPPORT THEOREM FOR PINNED DIFFUSION PROCESSES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 241-264
- Print publication:
- March 2024
-
- Article
- Export citation