Refine search
Actions for selected content:
15 results
ON THE SINGULARITIES OF QUOTIENTS BY 1-FOLIATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 30 June 2025, e6
- Print publication:
- 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Irrational rotations and
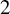 $2$-filling rays
$2$-filling rays
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 20 November 2024, pp. 1673-1697
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamical incoherence for a large class of partially hyperbolic diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 03 November 2020, pp. 3227-3243
- Print publication:
- November 2021
-
- Article
- Export citation
Lecture 1 - Closed Holomorphic Curves in Symplectic 4-Manifolds
-
- Book:
- Lectures on Contact 3-Manifolds, Holomorphic Curves and Intersection Theory
- Published online:
- 06 March 2020
- Print publication:
- 26 March 2020, pp 11-25
-
- Chapter
- Export citation
Higher-dimensional foliated Mori theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 14 November 2019, pp. 1-38
- Print publication:
- January 2020
-
- Article
- Export citation
Unique ergodicity of the horocycle flow on Riemannnian foliations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 13 November 2018, pp. 1459-1479
- Print publication:
- June 2020
-
- Article
- Export citation
Foliations on unitary Shimura varieties in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 11 October 2018, pp. 2267-2304
- Print publication:
- November 2018
-
- Article
- Export citation
An interesting example for spectral invariants
-
- Journal:
- Journal of K-Theory / Volume 13 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 03 April 2014, pp. 305-311
- Print publication:
- April 2014
-
- Article
- Export citation
On the AF-algebra of a Hecke eigenform
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 08 November 2011, pp. 207-213
-
- Article
-
- You have access
- Export citation
The analytic index of elliptic pseudodifferential operators on a singular foliation
-
- Journal:
- Journal of K-Theory / Volume 8 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 10 March 2011, pp. 363-385
- Print publication:
- December 2011
-
- Article
- Export citation
The K-theory of the C*-algebra of foliations by slope components
-
- Journal:
- Journal of K-Theory / Volume 3 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 28 May 2008, pp. 221-260
- Print publication:
- April 2009
-
- Article
- Export citation
On the local structure of Dirac manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 774-786
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
LAMINATIONS DANS LES ESPACES PROJECTIFS COMPLEXES
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 15 March 2007, pp. 67-91
- Print publication:
- January 2008
-
- Article
- Export citation
Foliations Leaf Through Economics
-
- Journal:
- Macroeconomic Dynamics / Volume 3 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 September 1999, pp. 384-426
-
- Article
- Export citation
Holonomy and basic cohomology of foliations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 3 / June 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-300
- Print publication:
- June 1996
-
- Article
-
- You have access
- Export citation



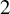
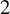
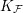
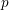
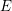
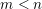
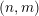
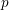
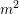
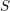
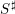
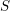
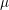
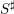
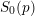
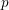
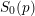
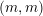
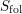
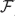 ). In the current paper we construct the analytic index of an elliptic operator as a
). In the current paper we construct the analytic index of an elliptic operator as a  on
on 