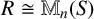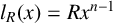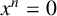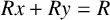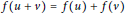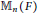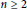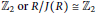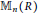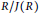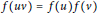Refine search
Actions for selected content:
10 results
14 - Insubordination at the Interaction of Discourse, Grammar, and Prosody
- from Part IV - Multimodality and Construction Grammar
-
-
- Book:
- The Cambridge Handbook of Construction Grammar
- Published online:
- 30 January 2025
- Print publication:
- 06 February 2025, pp 354-383
-
- Chapter
- Export citation
Association between protein intake, diet quality, and obesity in Australian adults: a comparison of measurement units
-
- Journal:
- Journal of Nutritional Science / Volume 13 / 2024
- Published online by Cambridge University Press:
- 20 September 2024, e42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CHARACTERISATION OF MATRIX RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 08 August 2022, pp. 95-101
- Print publication:
- February 2023
-
- Article
- Export citation
A NOTE ON GROUP RINGS WITH TRIVIAL UNITS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 19 July 2021, pp. 243-247
- Print publication:
- April 2022
-
- Article
- Export citation
Chapter 36 - Calculations for the Prescriber
- from Part 9 - Calculations
-
-
- Book:
- Surviving Prescribing
- Published online:
- 08 June 2020
- Print publication:
- 25 June 2020, pp 155-158
-
- Chapter
- Export citation
2 - Working with Mathematica
-
- Book:
- The Student's Introduction to <I>Mathematica</I> and the Wolfram Language
- Published online:
- 01 April 2019
- Print publication:
- 16 May 2019, pp 27-50
-
- Chapter
- Export citation
Additive Maps on Units of Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 1 / 01 March 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 130-141
- Print publication:
- 01 March 2018
-
- Article
-
- You have access
- Export citation
DECOMPOSING LINEAR TRANSFORMATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 14 September 2010, pp. 256-261
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
Tucson, One Year Later …1
-
- Journal:
- Radiocarbon / Volume 40 / Issue 2 / 1997
- Published online by Cambridge University Press:
- 18 July 2016, pp. iii-iv
- Print publication:
- 1997
-
- Article
-
- You have access
- Export citation
Nilpotents and units in skew polynomial rings over commutative rings
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 423-426
- Print publication:
- December 1979
-
- Article
-
- You have access
- Export citation