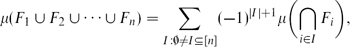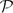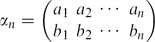Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
An Extension of the Hajnal–Szemerédi Theorem to Directed Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 5 / September 2015
- Published online by Cambridge University Press:
- 28 October 2014, pp. 754-773
-
- Article
- Export citation
Query Complexity of Sampling and Small Geometric Partitions
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 5 / September 2015
- Published online by Cambridge University Press:
- 21 October 2014, pp. 733-753
-
- Article
- Export citation
Sperner's Problem for G-Independent Families
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 3 / May 2015
- Published online by Cambridge University Press:
- 15 October 2014, pp. 528-550
-
- Article
- Export citation
Maximizing the Number of Independent Sets of a Fixed Size
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 3 / May 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 521-527
-
- Article
- Export citation
Simplifying Inclusion–Exclusion Formulas
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 2 / March 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 438-456
-
- Article
- Export citation
‘The Asymptotic Number of Connected d-Uniform Hypergraphs’ — CORRIGENDUM
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 373-375
-
- Article
-
- You have access
- Export citation
Diagonal Asymptotics for Products of Combinatorial Classes
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 10 October 2014, pp. 354-372
-
- Article
- Export citation
Evaluations of Topological Tutte Polynomials
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 3 / May 2015
- Published online by Cambridge University Press:
- 10 October 2014, pp. 556-583
-
- Article
- Export citation
Optimal Codes in the Enomoto-Katona Space
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 2 / March 2015
- Published online by Cambridge University Press:
- 09 October 2014, pp. 382-406
-
- Article
- Export citation
Set Systems Containing Many Maximal Chains
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 3 / May 2015
- Published online by Cambridge University Press:
- 09 October 2014, pp. 480-485
-
- Article
- Export citation
A Binary Deletion Channel With a Fixed Number of Deletions
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 3 / May 2015
- Published online by Cambridge University Press:
- 07 October 2014, pp. 486-489
-
- Article
- Export citation
CPC volume 23 issue 6 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 6 / November 2014
- Published online by Cambridge University Press:
- 06 October 2014, pp. b1-b8
-
- Article
-
- You have access
- Export citation
CPC volume 23 issue 6 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 6 / November 2014
- Published online by Cambridge University Press:
- 06 October 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Near Perfect Matchings in k-Uniform Hypergraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 5 / September 2015
- Published online by Cambridge University Press:
- 02 October 2014, pp. 723-732
-
- Article
- Export citation
Resolution of T. Ward's Question and the Israel–Finch Conjecture: Precise Analysis of an Integer Sequence Arising in Dynamics
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 02 October 2014, pp. 195-215
-
- Article
- Export citation
Quantitative Equidistribution for Certain Quadruples in Quasi-Random Groups
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 2 / March 2015
- Published online by Cambridge University Press:
- 02 October 2014, pp. 376-381
-
- Article
- Export citation
An Alternative Proof of the Linearity of the Size-Ramsey Number of Paths
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 3 / May 2015
- Published online by Cambridge University Press:
- 02 October 2014, pp. 551-555
-
- Article
- Export citation
Improved Bounds for Incidences Between Points and Circles
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 3 / May 2015
- Published online by Cambridge University Press:
- 02 October 2014, pp. 490-520
-
- Article
- Export citation
Longest Increasing Subsequences of Randomly Chosen Multi-Row Arrays
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 02 October 2014, pp. 254-293
-
- Article
- Export citation
Loose Hamilton Cycles in Regular Hypergraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 24 September 2014, pp. 179-194
-
- Article
- Export citation