Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
The Size of a Hypergraph and its Matching Number
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 20 January 2012, pp. 442-450
-
- Article
- Export citation
Order-Invariant Measures on Fixed Causal Sets
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 19 January 2012, pp. 330-357
-
- Article
- Export citation
On the Banach-Space-Valued Azuma Inequality and Small-Set Isoperimetry of Alon–Roichman Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 18 January 2012, pp. 623-634
-
- Article
- Export citation
Approximating Cayley Diagrams Versus Cayley Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 04 January 2012, pp. 635-641
-
- Article
- Export citation
Special issue dedicated to the thirteenth"Journées Montoises d'Informatique Théorique"
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 13 February 2012, p. 1
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
Morphisms preserving the set of words coding three intervalexchange∗∗∗
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 21 February 2012, pp. 107-122
- Print publication:
- January 2012
-
- Article
- Export citation
Job shop scheduling with unit length tasks
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 21 December 2011, pp. 329-342
- Print publication:
- July 2012
-
- Article
- Export citation
Frontmatter
-
- Book:
- Enumerative Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 12 December 2011, pp i-vi
-
- Chapter
- Export citation
4 - Rational Generating Functions
-
- Book:
- Enumerative Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 12 December 2011, pp 464-570
-
- Chapter
- Export citation
First Edition Numbering
-
- Book:
- Enumerative Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 12 December 2011, pp 575-580
-
- Chapter
- Export citation
List of Notation (Partial)
-
- Book:
- Enumerative Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 12 December 2011, pp 581-584
-
- Chapter
- Export citation
Appendix: Graph Theory Terminology
-
- Book:
- Enumerative Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 12 December 2011, pp 571-574
-
- Chapter
- Export citation
Index
-
- Book:
- Enumerative Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 12 December 2011, pp 585-626
-
- Chapter
- Export citation
1 - What Is Enumerative Combinatorics?
-
- Book:
- Enumerative Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 12 December 2011, pp 1-194
-
- Chapter
- Export citation
Contents
-
- Book:
- Enumerative Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 12 December 2011, pp vii-x
-
- Chapter
- Export citation
3 - Partially Ordered Sets
-
- Book:
- Enumerative Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 12 December 2011, pp 241-463
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Enumerative Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 12 December 2011, pp xiii-xiv
-
- Chapter
- Export citation
2 - Sieve Methods
-
- Book:
- Enumerative Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 12 December 2011, pp 195-240
-
- Chapter
- Export citation
Preface
-
- Book:
- Enumerative Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 12 December 2011, pp xi-xii
-
- Chapter
- Export citation
The Turán Number of F3,3
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 29 November 2011, pp. 451-456
-
- Article
- Export citation
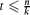 , every
, every 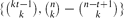 edges. Although this appears to be a basic instance of the hypergraph Turán problem (with a
edges. Although this appears to be a basic instance of the hypergraph Turán problem (with a 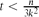 . This improves upon the best previously known range
. This improves upon the best previously known range 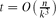 , which dates back to the 1970s.
, which dates back to the 1970s.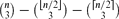 . This sharpens results of Zhou [9] and of the second author and Rödl [7].
. This sharpens results of Zhou [9] and of the second author and Rödl [7].