Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Linear spans of optimal sets of frequency hopping sequences∗
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 343-354
- Print publication:
- July 2012
-
- Article
- Export citation
On the size of transducers for bidirectional decoding of prefixcodes
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 315-328
- Print publication:
- April 2012
-
- Article
- Export citation
Easy lambda-terms are not always simple
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 291-314
- Print publication:
- April 2012
-
- Article
- Export citation
Foreword ICTCS 2010 special issue
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 21 February 2012, p. 201
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
Formal Methods to Improve Public Administration BusinessProcesses
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 21 February 2012, pp. 203-229
- Print publication:
- April 2012
-
- Article
- Export citation

Infinite Electrical Networks
-
- Published online:
- 05 February 2012
- Print publication:
- 29 November 1991

A Guide to Experimental Algorithmics
-
- Published online:
- 05 February 2012
- Print publication:
- 30 January 2012
Minimum Degree and Disjoint Cycles in Claw-Free Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 129-139
-
- Article
- Export citation
Homeomorphically Irreducible Spanning Trees in Locally Connected Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 107-111
-
- Article
- Export citation
Edge Colourings of Graphs Avoiding Monochromatic Matchings of a Given Size
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 203-218
-
- Article
- Export citation
Hypergraphs with No Cycle of a Given Length
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 193-201
-
- Article
- Export citation
A Pair of Forbidden Subgraphs and 2-Factors
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 149-158
-
- Article
- Export citation
Most Probably Intersecting Families of Subsets
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 219-227
-
- Article
- Export citation
Critical Probabilities of 1-Independent Percolation Models
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 11-22
-
- Article
- Export citation
The Phase Transition in the Configuration Model
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 265-299
-
- Article
- Export citation
List Colourings of Regular Hypergraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 315-322
-
- Article
- Export citation
2-Cancellative Hypergraphs and Codes
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 159-177
-
- Article
- Export citation
Large Rainbow Matchings in Edge-Coloured Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 255-263
-
- Article
- Export citation
Degree Ramsey Numbers of Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 229-253
-
- Article
- Export citation
Corrádi and Hajnal's Theorem for Sparse Random Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 23-55
-
- Article
- Export citation

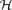
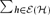
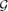
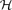
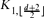 -free graph of minimum degree at least
-free graph of minimum degree at least 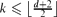 every connected graph
every connected graph 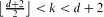 , and prove that only a finite number of connected graphs
, and prove that only a finite number of connected graphs 
 -element subsets. We determine the most probably inclusion-free family too, when the number of members is
-element subsets. We determine the most probably inclusion-free family too, when the number of members is  .
.