Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
On Even-Degree Subgraphs of Linear Hypergraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 113-127
-
- Article
- Export citation
Star Versus Two Stripes Ramsey Numbers and a Conjecture of Schelp
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 179-186
-
- Article
- Export citation
The Maximum Number of Triangles in C2k+1-Free Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 187-191
-
- Article
- Export citation
Degree Powers in Graphs: The Erdős–Stone Theorem
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 89-105
-
- Article
- Export citation
My Friend and Colleague, Richard Schelp
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 1-9
-
- Article
- Export citation
On the Maximum Number of Edges in a Triple System Not Containing a Disjoint Family of a Given Size
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 141-148
-
- Article
- Export citation
Compressions and Probably Intersecting Families
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 301-313
-
- Article
- Export citation
Contents
-
- Book:
- A Guide to Experimental Algorithmics
- Published online:
- 05 February 2012
- Print publication:
- 30 January 2012, pp vii-viii
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- A Guide to Experimental Algorithmics
- Published online:
- 05 February 2012
- Print publication:
- 30 January 2012, pp i-vi
-
- Chapter
- Export citation
6 - Creating Analysis-Friendly Data
-
- Book:
- A Guide to Experimental Algorithmics
- Published online:
- 05 February 2012
- Print publication:
- 30 January 2012, pp 181-214
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- A Guide to Experimental Algorithmics
- Published online:
- 05 February 2012
- Print publication:
- 30 January 2012, pp 1-16
-
- Chapter
- Export citation
4 - Tuning Algorithms, Tuning Code
-
- Book:
- A Guide to Experimental Algorithmics
- Published online:
- 05 February 2012
- Print publication:
- 30 January 2012, pp 98-151
-
- Chapter
- Export citation
Preface
-
- Book:
- A Guide to Experimental Algorithmics
- Published online:
- 05 February 2012
- Print publication:
- 30 January 2012, pp ix-x
-
- Chapter
- Export citation
3 - What to Measure
-
- Book:
- A Guide to Experimental Algorithmics
- Published online:
- 05 February 2012
- Print publication:
- 30 January 2012, pp 50-97
-
- Chapter
- Export citation
2 - A Plan of Attack
-
- Book:
- A Guide to Experimental Algorithmics
- Published online:
- 05 February 2012
- Print publication:
- 30 January 2012, pp 17-49
-
- Chapter
- Export citation
7 - Data Analysis
-
- Book:
- A Guide to Experimental Algorithmics
- Published online:
- 05 February 2012
- Print publication:
- 30 January 2012, pp 215-256
-
- Chapter
- Export citation
5 - The Toolbox
-
- Book:
- A Guide to Experimental Algorithmics
- Published online:
- 05 February 2012
- Print publication:
- 30 January 2012, pp 152-180
-
- Chapter
- Export citation
Index
-
- Book:
- A Guide to Experimental Algorithmics
- Published online:
- 05 February 2012
- Print publication:
- 30 January 2012, pp 257-261
-
- Chapter
- Export citation
Cliques in Graphs With Bounded Minimum Degree
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 26 January 2012, pp. 457-482
-
- Article
- Export citation
Limit Theorems for Subtree Size Profiles of Increasing Trees
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 25 January 2012, pp. 412-441
-
- Article
- Export citation
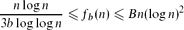

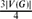 , then in every 2-colouring of the edges of
, then in every 2-colouring of the edges of 





