Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Unit Distances in Three Dimensions
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 25 April 2012, pp. 597-610
-
- Article
- Export citation
Distance Preserving Ramsey Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 23 April 2012, pp. 554-581
-
- Article
- Export citation
k-Sums in Abelian Groups
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 23 April 2012, pp. 582-596
-
- Article
- Export citation
Conflict-Free Colourings of Uniform Hypergraphs With Few Edges
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 20 April 2012, pp. 611-622
-
- Article
- Export citation
CPC volume 21 issue 3 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Some Properties of Lower Level-Sets of Convolutions
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 515-530
-
- Article
- Export citation
CPC volume 21 issue 3 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. f1-f2
-
- Article
-
- You have access
- Export citation
On the joint 2-adic complexity of binary multisequences∗
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 06 April 2012, pp. 401-412
- Print publication:
- July 2012
-
- Article
- Export citation
Set Families With a Forbidden Induced Subposet
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 22 March 2012, pp. 496-511
-
- Article
- Export citation
Scott's Induced Subdivision Conjecture for Maximal Triangle-Free Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 21 March 2012, pp. 512-514
-
- Article
- Export citation
Monochromatic Cycles in 2-Coloured Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. 57-87
-
- Article
- Export citation
CPC volume 21 issue 1-2 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. f1-f2
-
- Article
-
- You have access
- Export citation
CPC volume 21 issue 1-2 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. b1-b8
-
- Article
-
- You have access
- Export citation
Space Crossing Numbers
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 16 March 2012, pp. 358-373
-
- Article
- Export citation
Non-Three-Colourable Common Graphs Exist
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 16 March 2012, pp. 734-742
-
- Article
- Export citation
Measurable Events Indexed by Trees
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 12 March 2012, pp. 374-411
-
- Article
- Export citation
Equivalences and Congruences on Infinite Conway Games∗
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 02 March 2012, pp. 231-259
- Print publication:
- April 2012
-
- Article
- Export citation
The Density Turán Problem
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 29 February 2012, pp. 531-553
-
- Article
- Export citation
Detachments of Hypergraphs I: The Berge–Johnson Problem
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 27 February 2012, pp. 483-495
-
- Article
- Export citation
A graphical representation of relational formulae withcomplementation∗
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 27 February 2012, pp. 261-289
- Print publication:
- April 2012
-
- Article
- Export citation
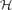

 . This extends a result of Bukh [1], which in turn generalizes several known results including Sperner's theorem.
. This extends a result of Bukh [1], which in turn generalizes several known results including Sperner's theorem.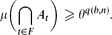

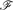
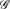
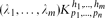 be a hypergraph with vertex partition {
be a hypergraph with vertex partition {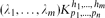 to be expressed as the union
to be expressed as the union 