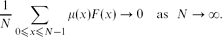Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
PART TWO - FOUNDATIONS
-
- Book:
- Dense Sphere Packings
- Published online:
- 05 October 2012
- Print publication:
- 06 September 2012, pp 23-24
-
- Chapter
- Export citation
6 - Packing
- from PART THREE - THE KEPLER CONJECTURE
-
- Book:
- Dense Sphere Packings
- Published online:
- 05 October 2012
- Print publication:
- 06 September 2012, pp 145-193
-
- Chapter
- Export citation
PART ONE - OVERVIEW
-
- Book:
- Dense Sphere Packings
- Published online:
- 05 October 2012
- Print publication:
- 06 September 2012, pp 1-2
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Dense Sphere Packings
- Published online:
- 05 October 2012
- Print publication:
- 06 September 2012, pp i-iv
-
- Chapter
- Export citation
Preface
-
- Book:
- Dense Sphere Packings
- Published online:
- 05 October 2012
- Print publication:
- 06 September 2012, pp vii-xiv
-
- Chapter
- Export citation
General index
-
- Book:
- Dense Sphere Packings
- Published online:
- 05 October 2012
- Print publication:
- 06 September 2012, pp 264-268
-
- Chapter
- Export citation
5 - Fan
- from PART TWO - FOUNDATIONS
-
- Book:
- Dense Sphere Packings
- Published online:
- 05 October 2012
- Print publication:
- 06 September 2012, pp 112-142
-
- Chapter
- Export citation
3 - Volume
- from PART TWO - FOUNDATIONS
-
- Book:
- Dense Sphere Packings
- Published online:
- 05 October 2012
- Print publication:
- 06 September 2012, pp 61-71
-
- Chapter
- Export citation
Contents
-
- Book:
- Dense Sphere Packings
- Published online:
- 05 October 2012
- Print publication:
- 06 September 2012, pp v-vi
-
- Chapter
- Export citation
On (Not) Computing the Möbius Function Using Bounded Depth Circuits
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 24 August 2012, pp. 942-951
-
- Article
- Export citation
Cops and Robbers on Geometric Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 16 August 2012, pp. 816-834
-
- Article
- Export citation
Testing Odd-Cycle-Freeness in Boolean Functions
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 10 August 2012, pp. 835-855
-
- Article
- Export citation

Modern Computer Arithmetic
-
- Published online:
- 05 August 2012
- Print publication:
- 25 November 2010
On Sums of Generating Sets in ℤ2n
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 03 August 2012, pp. 916-941
-
- Article
- Export citation
Affine Parikh automata∗
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 02 August 2012, pp. 511-545
- Print publication:
- October 2012
-
- Article
- Export citation
Normal forms for unary probabilistic automata
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 02 August 2012, pp. 495-510
- Print publication:
- October 2012
-
- Article
- Export citation
Regularity of languages defined by formal series with isolatedcut point∗
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 02 August 2012, pp. 479-493
- Print publication:
- October 2012
-
- Article
- Export citation
String Assembling Systems
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 02 August 2012, pp. 593-613
- Print publication:
- October 2012
-
- Article
- Export citation
Generating Networks of Splicing Processors
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 46 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 30 July 2012, pp. 547-572
- Print publication:
- October 2012
-
- Article
- Export citation
Connectivity for Bridge-Addable Monotone Graph Classes
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 30 July 2012, pp. 803-815
-
- Article
- Export citation