Refine search
Actions for selected content:
48202 results in Computer Science
The minimal generating sets of
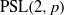 $\mathrm{PSL} (2, p)$ of size four
$\mathrm{PSL} (2, p)$ of size four
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 06 November 2013, pp. 419-423
-
- Article
-
- You have access
- Export citation
Component Games on Regular Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 04 November 2013, pp. 75-89
-
- Article
- Export citation
Short Proofs of Some Extremal Results
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 04 November 2013, pp. 8-28
-
- Article
- Export citation
Infinite probability computation by cyclic explanation graphs
-
- Journal:
- Theory and Practice of Logic Programming / Volume 14 / Issue 6 / November 2014
- Published online by Cambridge University Press:
- 04 November 2013, pp. 909-937
-
- Article
- Export citation
LOGICAL GROUNDS
-
- Journal:
- The Review of Symbolic Logic / Volume 7 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 04 November 2013, pp. 31-59
- Print publication:
- March 2014
-
- Article
- Export citation
ROB volume 31 issue 8 Cover and Back matter
-
- Article
-
- You have access
- Export citation
ROB volume 31 issue 8 Cover and Front matter
-
- Article
-
- You have access
- Export citation
Local computability and uncountable structures
-
-
- Book:
- Effective Mathematics of the Uncountable
- Published online:
- 05 December 2013
- Print publication:
- 31 October 2013, pp 81-123
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Effective Mathematics of the Uncountable
- Published online:
- 05 December 2013
- Print publication:
- 31 October 2013, pp i-iv
-
- Chapter
- Export citation
Effective model theory: approach via σ-definability
-
-
- Book:
- Effective Mathematics of the Uncountable
- Published online:
- 05 December 2013
- Print publication:
- 31 October 2013, pp 164-197
-
- Chapter
- Export citation
Contents
-
- Book:
- Effective Mathematics of the Uncountable
- Published online:
- 05 December 2013
- Print publication:
- 31 October 2013, pp v-vi
-
- Chapter
- Export citation
Reverse mathematics, countable and uncountable: a computational approach
-
-
- Book:
- Effective Mathematics of the Uncountable
- Published online:
- 05 December 2013
- Print publication:
- 31 October 2013, pp 150-163
-
- Chapter
- Export citation
Borel structures: a brief survey
-
-
- Book:
- Effective Mathematics of the Uncountable
- Published online:
- 05 December 2013
- Print publication:
- 31 October 2013, pp 124-134
-
- Chapter
- Export citation
Computable structure theory using admissible recursion theory on ω1 using admissibility
-
-
- Book:
- Effective Mathematics of the Uncountable
- Published online:
- 05 December 2013
- Print publication:
- 31 October 2013, pp 50-80
-
- Chapter
- Export citation
Introduction
-
- Book:
- Effective Mathematics of the Uncountable
- Published online:
- 05 December 2013
- Print publication:
- 31 October 2013, pp 1-13
-
- Chapter
- Export citation
Some results on ℝ-computable structures
-
-
- Book:
- Effective Mathematics of the Uncountable
- Published online:
- 05 December 2013
- Print publication:
- 31 October 2013, pp 14-32
-
- Chapter
- Export citation
Infinite time Turing machines and an application to the hierarchy of equivalence relations on the reals
-
-
- Book:
- Effective Mathematics of the Uncountable
- Published online:
- 05 December 2013
- Print publication:
- 31 October 2013, pp 33-49
-
- Chapter
- Export citation
E-recursive intuitions
-
-
- Book:
- Effective Mathematics of the Uncountable
- Published online:
- 05 December 2013
- Print publication:
- 31 October 2013, pp 135-149
-
- Chapter
- Export citation
Preface
-
- Book:
- Effective Mathematics of the Uncountable
- Published online:
- 05 December 2013
- Print publication:
- 31 October 2013, pp vii-viii
-
- Chapter
- Export citation