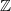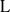Refine search
Actions for selected content:
48285 results in Computer Science
Single-class genera of positive integral lattices
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 172-186
-
- Article
-
- You have access
- Export citation
Explicit application of Waldspurger’s theorem
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 216-245
-
- Article
-
- You have access
- Export citation
Computing level one Hecke eigensystems (mod
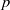 $p$ )
$p$ )
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 246-270
-
- Article
-
- You have access
- Export citation
Modular subgroups, dessins d’enfants and elliptic K3 surfaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 271-318
-
- Article
-
- You have access
- Export citation
The decomposed affiliation exposure model: A network approach to segregating peer influences from crowds and organized sports
-
- Journal:
- Network Science / Volume 1 / Issue 2 / August 2013
- Published online by Cambridge University Press:
- 30 July 2013, pp. 154-169
-
- Article
-
- You have access
- Open access
- Export citation
Unsupervised acquisition of entailment relations from the Web
-
- Journal:
- Natural Language Engineering / Volume 21 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 30 July 2013, pp. 3-47
-
- Article
- Export citation
A variable neighborhood search method for a two-mode blockmodeling problem in social network analysis
-
- Journal:
- Network Science / Volume 1 / Issue 2 / August 2013
- Published online by Cambridge University Press:
- 30 July 2013, pp. 191-212
-
- Article
- Export citation
Diagrams in biology
-
- Journal:
- The Knowledge Engineering Review / Volume 28 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 30 July 2013, pp. 273-286
-
- Article
- Export citation
Thinking through drawing: Diagram constructions as epistemic mediators in geometrical discovery
-
- Journal:
- The Knowledge Engineering Review / Volume 28 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 30 July 2013, pp. 303-326
-
- Article
- Export citation
Independence-Friendly Logic: A Game-Theoretic Approach, Allen L. Mann , Gabriel Sanduand Merlijn Sevenster , Cambridge University Press, 2011. Paperback, ISBN 9780521149341, 216 pp.
-
- Journal:
- Theory and Practice of Logic Programming / Volume 14 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 30 July 2013, pp. 137-140
-
- Article
- Export citation
Engineering social contagions: Optimal network seeding in the presence of homophily
-
- Journal:
- Network Science / Volume 1 / Issue 2 / August 2013
- Published online by Cambridge University Press:
- 30 July 2013, pp. 125-153
-
- Article
-
- You have access
- Export citation
8 - Controlled Simulation Analysis
-
- Book:
- Excel Basics to Blackbelt
- Published online:
- 05 August 2013
- Print publication:
- 29 July 2013, pp 207-244
-
- Chapter
- Export citation
5 - Simplification Tactics
-
- Book:
- Excel Basics to Blackbelt
- Published online:
- 05 August 2013
- Print publication:
- 29 July 2013, pp 106-139
-
- Chapter
- Export citation
Section 2 - Harvesting Intelligence
-
- Book:
- Excel Basics to Blackbelt
- Published online:
- 05 August 2013
- Print publication:
- 29 July 2013, pp 61-62
-
- Chapter
- Export citation
7 - Complex Optimization
-
- Book:
- Excel Basics to Blackbelt
- Published online:
- 05 August 2013
- Print publication:
- 29 July 2013, pp 177-204
-
- Chapter
- Export citation
Section 3 - Leveraging Dynamic Analysis
-
- Book:
- Excel Basics to Blackbelt
- Published online:
- 05 August 2013
- Print publication:
- 29 July 2013, pp 205-206
-
- Chapter
- Export citation
Appendix: Shortcut (Hot Key) Reference
-
- Book:
- Excel Basics to Blackbelt
- Published online:
- 05 August 2013
- Print publication:
- 29 July 2013, pp 389-390
-
- Chapter
- Export citation
Preface
-
-
- Book:
- Excel Basics to Blackbelt
- Published online:
- 05 August 2013
- Print publication:
- 29 July 2013, pp xi-xii
-
- Chapter
- Export citation
Glossary of Key Terms
-
- Book:
- Excel Basics to Blackbelt
- Published online:
- 05 August 2013
- Print publication:
- 29 July 2013, pp 381-388
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Excel Basics to Blackbelt
- Published online:
- 05 August 2013
- Print publication:
- 29 July 2013, pp i-iv
-
- Chapter
- Export citation