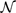In intuitionistic analysis, a subset of a Polish space like ℝ or is called positively Borel if and only if it is an open subset of the space or a closed subset of the space or the result of forming either the countable union or the countable intersection of an infinite sequence of (earlier constructed) positively Borel subsets of the space. The operation of taking the complement is absent from this inductive definition, and, in fact, the complement of a positively Borel set is not always positively Borel itself (see Veldman, 2008a). The main result of Veldman (2008a) is that, assuming Brouwer's Continuity Principle and an Axiom of Countable Choice, one may prove that the hierarchy formed by the positively Borel sets is genuinely growing: every level of the hierarchy contains sets that do not occur at any lower level. The purpose of the present paper is a different one: we want to explore the truly remarkable fine structure of the hierarchy. Brouwer's Continuity Principle again is our main tool. A second axiom proposed by Brouwer, his Thesis on Bars is also used, but only incidentally.

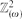Given ω ≥ 1, let be the graph with vertex set 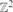in which two vertices are joined if they agree in one coordinate and differ by at most ω in the other. (Thus 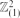is precisely .) Let pc(ω) be the critical probability for site percolation on . Extending recent results of Frieze, Kleinberg, Ravi and Debany, we show that limω→∞ωpc(ω)=log(3/2). We also prove analogues of this result for the n-by-n grid and in higher dimensions, the latter involving interesting connections to Gilbert's continuum percolation model. To prove our results, we explore the component of the origin in a certain non-standard way, and show that this exploration is well approximated by a certain branching random walk.

This paper deals with the perception mode of smart wheelchairs. First we evoke the many mobility aid prototypes developed in rehabilitation robotics by considering the point of view of perception. Then we describe the localization mode of the VAHM**. We show how the odometric, ultrasound, and vision sensors are used in a complementary way in order to locate the wheelchair in its known environment. The mode of adjustment of the odometric position by the least-squared method using ultrasonic measurements is detailed. Then the use of vision to perceive the vertical segments of the environment so as to refine the orientation is presented. The results of the tests carried out on the wheelchair are given and commented.

Component-based development (CBD) has become an important emerging topic in the software engineering field. It promises long-sought-after benefits such as increased software reuse, reduced development time to market and, hence, reduced software production cost. Despite the huge potential, the lack of reasoning support and development environment of component modeling and verification may hinder its development. Methods and tools that can support component model analysis are highly appreciated by industry. Such a tool support should be fully automated as well as efficient. At the same time, the reasoning tool should scale up well as it may need to handle hundreds or even thousands of components that a modern software system may have. Furthermore, a distributed environment that can effectively manage and compose components is also desirable. In this paper, we present an approach to the modeling and verification of a newly proposed component model using Semantic Web languages and their reasoning tools. We use the Web Ontology Language and the Semantic Web Rule Language to precisely capture the inter-relationships and constraints among the entities in a component model. Semantic Web reasoning tools are deployed to perform automated analysis support of the component models. Moreover, we also proposed a service-oriented architecture (SOA)-based semantic web environment for CBD. The adoption of Semantic Web services and SOA make our component environment more reusable, scalable, dynamic and adaptive.

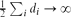Consider a random multigraph G* with given vertex degrees d1,. . .,dn, constructed by the configuration model. We show that, asymptotically for a sequence of such multigraphs with the number of edges , the probability that the multigraph is simple stays away from 0 if and only if 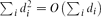. This was previously known only under extra assumptions on the maximum degree maxidi. We also give an asymptotic formula for this probability, extending previous results by several authors.

Relevance logics are known to be sound and complete for relational semantics with a ternary accessibility relation. This paper investigates the problem of adequacy with respect to special kinds of dynamic semantics (i.e., proper relation algebras and relevant families of relations). We prove several soundness results here. We also prove the completeness of a certain positive fragment of R as well as of the first-degree fragment of relevance logics. These results show that some core ideas are shared between relevance logics and relation algebras. Some details of certain incompleteness results, however, pinpoint where relevance logics and relation algebras diverge. To carry out these semantic investigations, we define a new tableaux formalization and new sequent calculi (with the single cut rule admissible) for various relevance logics.

There is a minor error in Section 3 wherein it is stated that ∖acc 0_ _ k loops in_nitely, even if k succeeds on input _.” This statement is not correct, and should be replaced by ∖If k returns false on input cs, then acc 1_ cs k loops in_nitely.”

The author is grateful to Derek Dreyer for pointing out this mistake, and suggesting the above-mentioned correction.

Jim Propp's rotor–router model is a deterministic analogue of a random walk on a graph. Instead of distributing chips randomly, each vertex serves its neighbours in a fixed order. We analyse the difference between the Propp machine and random walk on the infinite two-dimensional grid. It is known that, apart from a technicality, independent of the starting configuration, at each time the number of chips on each vertex in the Propp model deviates from the expected number of chips in the random walk model by at most a constant. We show that this constant is approximately 7.8 if all vertices serve their neighbours in clockwise or order, and 7.3 otherwise. This result in particular shows that the order in which the neighbours are served makes a difference. Our analysis also reveals a number of further unexpected properties of the two-dimensional Propp machine.

In majority bootstrap percolation on a graph G, an infection spreads according to the following deterministic rule: if at least half of the neighbours of a vertex v are already infected, then v is also infected, and infected vertices remain infected forever. We say that percolation occurs if eventually every vertex is infected.

The elements of the set of initially infected vertices, A ⊂ V(G), are normally chosen independently at random, each with probability p, say. This process has been extensively studied on the sequence of torus graphs [n]d, for n = 1,2, . . ., where d = d(n) is either fixed or a very slowly growing function of n. For example, Cerf and Manzo [17] showed that the critical probability is o(1) if d(n) ≤ log*n, i.e., if p = p(n) is bounded away from zero then the probability of percolation on [n]d tends to one as n → ∞.

In this paper we study the case when the growth of d to ∞ is not excessively slow; in particular, we show that the critical probability is 1/2 + o(1) if d ≥ (log log n)2 log log log n, and give much stronger bounds in the case that G is the hypercube, [2]d.

Macros still haven't made their way into typed higher-order programming languages such as Haskell and Standard ML. Therefore, to extend the expressiveness of Haskell or Standard ML, one must express new linguistic features in terms of functions that fit within the static type systems of these languages. This is particularly challenging when introducing features that span across multiple types and that bind variables. We address this challenge by developing, in a step by step manner, mechanisms for encoding patterns and pattern matching in Haskell in a type-safe way.

The paper offers a matrix-based logic (relevant matrix quantum physics) for propositions which seems suitable as an underlying logic for empirical sciences and especially for quantum physics. This logic is motivated by two criteria which serve to clean derivations of classical logic from superfluous redundancies and uninformative complexities. It distinguishes those valid derivations (inferences) of classical logic which contain superfluous redundancies and complexities and are in this sense “irrelevant” from those which are “relevant” or “nonredundant” in the sense of allowing only the most informative consequences in the derivations. The latter derivations are strictly valid in RMQ, whereas the former are only materially valid. RMQ is a decidable matrix calculus which possesses a semantics and has the finite model property. It is shown in the paper how RMQ by its strictly valid derivations can avoid the difficulties with commensurability, distributivity, and Bell's inequalities when it is applied to quantum physics.

We describe a lower bound for the rank of any real matrix in which all diagonal entries are significantly larger in absolute value than all other entries, and discuss several applications of this result to the study of problems in Geometry, Coding Theory, Extremal Finite Set Theory and Probability. This is partly a survey, containing a unified approach for proving various known results, but it contains several new results as well.