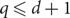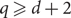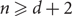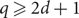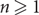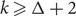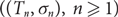Refine search
Actions for selected content:
48529 results in Computer Science
PROBABILISTIC STABILITY, AGM REVISION OPERATORS AND MAXIMUM ENTROPY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 October 2020, pp. 553-590
- Print publication:
- September 2022
-
- Article
- Export citation
On the impact of network size and average degree on the robustness of centrality measures
-
- Journal:
- Network Science / Volume 9 / Issue S1 / October 2021
- Published online by Cambridge University Press:
- 20 October 2020, pp. S61-S82
-
- Article
-
- You have access
- Open access
- Export citation

The Cambridge Handbook of the Law of Algorithms
-
- Published online:
- 19 October 2020
- Print publication:
- 05 November 2020

Wireless Edge Caching
- Modeling, Analysis, and Optimization
-
- Published online:
- 19 October 2020
- Print publication:
- 11 March 2021
Forward analysis for WSTS, part I: completions
-
- Journal:
- Mathematical Structures in Computer Science / Volume 30 / Issue 7 / August 2020
- Published online by Cambridge University Press:
- 19 October 2020, pp. 752-832
-
- Article
- Export citation
Sensitivity analysis for network observations with applications to inferences of social influence effects
-
- Journal:
- Network Science / Volume 9 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 19 October 2020, pp. 73-98
-
- Article
- Export citation
From industry-wide parameters to aircraft-centric on-flight inference: Improving aeronautics performance prediction with machine learning
-
- Journal:
- Data-Centric Engineering / Volume 1 / 2020
- Published online by Cambridge University Press:
- 19 October 2020, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mixing properties of colourings of the ℤd lattice
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 19 October 2020, pp. 360-373
-
- Article
- Export citation
Frozen (Δ + 1)-colourings of bounded degree graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 19 October 2020, pp. 330-343
-
- Article
- Export citation
A non-increasing tree growth process for recursive trees and applications
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 19 October 2020, pp. 79-104
-
- Article
- Export citation
Isolation concepts applied to temporal clique enumeration
-
- Journal:
- Network Science / Volume 9 / Issue S1 / October 2021
- Published online by Cambridge University Press:
- 16 October 2020, pp. S83-S105
-
- Article
- Export citation
Enhancing industrial X-ray tomography by data-centric statistical methods
-
- Journal:
- Data-Centric Engineering / Volume 1 / 2020
- Published online by Cambridge University Press:
- 16 October 2020, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
3 - Document Sentiment Classification
-
- Book:
- Sentiment Analysis
- Published online:
- 23 September 2020
- Print publication:
- 15 October 2020, pp 55-88
-
- Chapter
- Export citation
9 - A Framework for Cyber-Physical System Security Situation Awareness
- from Part III - Privacy, Security, and Protection
-
- Book:
- Principles of Cyber-Physical Systems
- Published online:
- 12 October 2020
- Print publication:
- 15 October 2020, pp 229-251
-
- Chapter
- Export citation
Bibliography
-
- Book:
- Sentiment Analysis
- Published online:
- 23 September 2020
- Print publication:
- 15 October 2020, pp 376-426
-
- Chapter
- Export citation
Preface
-
- Book:
- Sentiment Analysis
- Published online:
- 23 September 2020
- Print publication:
- 15 October 2020, pp xi-xv
-
- Chapter
- Export citation
Contents
-
- Book:
- Principles of Cyber-Physical Systems
- Published online:
- 12 October 2020
- Print publication:
- 15 October 2020, pp v-xii
-
- Chapter
- Export citation
10 - Analysis of Debates and Comments
-
- Book:
- Sentiment Analysis
- Published online:
- 23 September 2020
- Print publication:
- 15 October 2020, pp 273-293
-
- Chapter
- Export citation