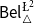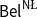Refine search
Actions for selected content:
48581 results in Computer Science
11 - Manipulation of Resources
- from Part III - The General Framework of Resource Theories
-
- Book:
- Quantum Resource Theories
- Published online:
- 03 May 2025
- Print publication:
- 10 April 2025, pp 467-504
-
- Chapter
- Export citation
5 - View from the Inside
-
- Book:
- Automated Agencies
- Published online:
- 03 April 2025
- Print publication:
- 10 April 2025, pp 95-109
-
- Chapter
- Export citation
4 - The Topological Representation Theorem
-
- Book:
- Oriented Matroids
- Published online:
- 04 June 2025
- Print publication:
- 10 April 2025, pp 103-135
-
- Chapter
- Export citation
10 - Quantification of Quantum Resources
- from Part III - The General Framework of Resource Theories
-
- Book:
- Quantum Resource Theories
- Published online:
- 03 May 2025
- Print publication:
- 10 April 2025, pp 426-466
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Quantum Resource Theories
- Published online:
- 03 May 2025
- Print publication:
- 10 April 2025, pp i-iv
-
- Chapter
- Export citation
7 - Conditional Entropy
- from Part II - Tools and Methods
-
- Book:
- Quantum Resource Theories
- Published online:
- 03 May 2025
- Print publication:
- 10 April 2025, pp 308-351
-
- Chapter
- Export citation
Dedication
-
- Book:
- Automated Agencies
- Published online:
- 03 April 2025
- Print publication:
- 10 April 2025, pp v-vi
-
- Chapter
- Export citation
8 - The Asymptotic Regime
- from Part II - Tools and Methods
-
- Book:
- Quantum Resource Theories
- Published online:
- 03 May 2025
- Print publication:
- 10 April 2025, pp 352-400
-
- Chapter
- Export citation
16 - The Resource Theory of Nonuniformity
- from Part V - Additional Examples of Static Resource Theories
-
- Book:
- Quantum Resource Theories
- Published online:
- 03 May 2025
- Print publication:
- 10 April 2025, pp 736-748
-
- Chapter
- Export citation
Two-layered logics for probabilities and belief functions over Belnap–Dunn logic
-
- Journal:
- Mathematical Structures in Computer Science / Volume 35 / 2025
- Published online by Cambridge University Press:
- 08 April 2025, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On calculating structural similarity metrics in population-based structural health monitoring
-
- Journal:
- Data-Centric Engineering / Volume 6 / 2025
- Published online by Cambridge University Press:
- 08 April 2025, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Principal types as partial involutions
-
- Journal:
- Mathematical Structures in Computer Science / Volume 35 / 2025
- Published online by Cambridge University Press:
- 08 April 2025, e8
-
- Article
- Export citation
Prior’s ideal language
-
- Journal:
- Mathematical Structures in Computer Science / Volume 35 / 2025
- Published online by Cambridge University Press:
- 08 April 2025, e7
-
- Article
- Export citation
On higher-order communication in ambient calculi
-
- Journal:
- Mathematical Structures in Computer Science / Volume 35 / 2025
- Published online by Cambridge University Press:
- 08 April 2025, e2
-
- Article
- Export citation
Data publishing in mechanics and dynamics: challenges, guidelines, and examples from engineering design
-
- Journal:
- Data-Centric Engineering / Volume 6 / 2025
- Published online by Cambridge University Press:
- 08 April 2025, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A classification of bisimilarities for general Markov decision processes
-
- Journal:
- Mathematical Structures in Computer Science / Volume 35 / 2025
- Published online by Cambridge University Press:
- 07 April 2025, e3
-
- Article
- Export citation
Joining forces for online feedback management: policy recommendations for human–AI collaboration
-
- Journal:
- Data & Policy / Volume 7 / 2025
- Published online by Cambridge University Press:
- 07 April 2025, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Temporal Vadalog System: Temporal Datalog-Based Reasoning
-
- Journal:
- Theory and Practice of Logic Programming / Volume 25 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 168-196
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The graphical theory of monads
- Part of
-
- Journal:
- Journal of Functional Programming / Volume 35 / 2025
- Published online by Cambridge University Press:
- 07 April 2025, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation