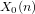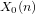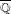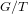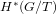Refine search
Actions for selected content:
48202 results in Computer Science
ON THE LOGIC OF FACTUAL EQUIVALENCE
-
- Journal:
- The Review of Symbolic Logic / Volume 9 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 07 August 2015, pp. 103-122
- Print publication:
- March 2016
-
- Article
-
- You have access
- Export citation
44 - Kronecker IV
- from PART SIX - Algebraic Solving
-
- Book:
- Solving Polynomial Equation Systems III
- Published online:
- 05 August 2015
- Print publication:
- 07 August 2015, pp 222-246
-
- Chapter
- Export citation
Isomorphism of intersection and union types†
-
- Journal:
- Mathematical Structures in Computer Science / Volume 27 / Issue 5 / June 2017
- Published online by Cambridge University Press:
- 07 August 2015, pp. 603-625
-
- Article
- Export citation
39 - Trinks
- from PART SIX - Algebraic Solving
-
- Book:
- Solving Polynomial Equation Systems III
- Published online:
- 05 August 2015
- Print publication:
- 07 August 2015, pp 3-18
-
- Chapter
- Export citation
Preface
-
- Book:
- Solving Polynomial Equation Systems III
- Published online:
- 05 August 2015
- Print publication:
- 07 August 2015, pp xi-xii
-
- Chapter
- Export citation
Taming the wild ant-lion; a counterexample to a conjecture of Böhm
-
- Journal:
- Mathematical Structures in Computer Science / Volume 27 / Issue 5 / June 2017
- Published online by Cambridge University Press:
- 07 August 2015, pp. 734-737
-
- Article
- Export citation
INFORMAL PROOF, FORMAL PROOF, FORMALISM
-
- Journal:
- The Review of Symbolic Logic / Volume 9 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 07 August 2015, pp. 23-43
- Print publication:
- March 2016
-
- Article
- Export citation
Index
-
- Book:
- Solving Polynomial Equation Systems III
- Published online:
- 05 August 2015
- Print publication:
- 07 August 2015, pp 273-275
-
- Chapter
- Export citation
Computational logics and verification techniques of multi-agent commitments: survey
-
- Journal:
- The Knowledge Engineering Review / Volume 30 / Issue 5 / November 2015
- Published online by Cambridge University Press:
- 06 August 2015, pp. 564-606
-
- Article
- Export citation
Understanding beginners' mistakes with Haskell
- Part of
-
- Journal:
- Journal of Functional Programming / Volume 25 / 2015
- Published online by Cambridge University Press:
- 06 August 2015, e11
-
- Article
-
- You have access
- Export citation

Solving Polynomial Equation Systems III
-
- Published online:
- 05 August 2015
- Print publication:
- 07 August 2015
Preface
-
- Journal:
- Mathematical Structures in Computer Science / Volume 27 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 05 August 2015, pp. 92-93
-
- Article
-
- You have access
- Export citation

Bayesian Speech and Language Processing
-
- Published online:
- 05 August 2015
- Print publication:
- 15 July 2015

Secure Multiparty Computation and Secret Sharing
-
- Published online:
- 05 August 2015
- Print publication:
- 15 July 2015

Inequalities for Graph Eigenvalues
-
- Published online:
- 05 August 2015
- Print publication:
- 23 July 2015
Modernising historical Slovene words
-
- Journal:
- Natural Language Engineering / Volume 22 / Issue 6 / November 2016
- Published online by Cambridge University Press:
- 03 August 2015, pp. 881-905
-
- Article
- Export citation
Examples of CM curves of genus two defined over the reflex field
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 August 2015, pp. 507-538
-
- Article
-
- You have access
- Export citation
Hyperelliptic modular curves
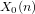 $X_{0}(n)$ and isogenies of elliptic curves over quadratic fields
$X_{0}(n)$ and isogenies of elliptic curves over quadratic fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 August 2015, pp. 578-602
-
- Article
-
- You have access
- Export citation
Schubert presentation of the cohomology ring of flag manifolds
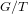 $G/T$
$G/T$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 August 2015, pp. 489-506
-
- Article
-
- You have access
- Export citation
Computing functions on Jacobians and their quotients
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 August 2015, pp. 555-577
-
- Article
-
- You have access
- Export citation