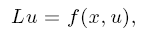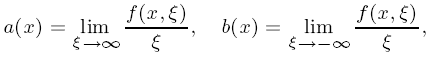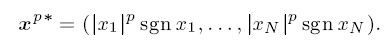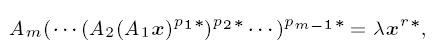Refine search
Actions for selected content:
25843 results in Abstract analysis
On conservation laws and necessary conditions in the calculus of variations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 132 / Issue 6 / December 2002
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1361-1371
- Print publication:
- December 2002
-
- Article
- Export citation
Existence of stationary solutions with transition layers for a class of cross-diffusion systems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 132 / Issue 6 / December 2002
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1493-1511
- Print publication:
- December 2002
-
- Article
- Export citation
Lagrangian and Hamiltonian formalism for constrained variational problems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 132 / Issue 6 / December 2002
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1417-1437
- Print publication:
- December 2002
-
- Article
- Export citation
Nonlinear eigenvalue problems for a class of ordinary differential equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 132 / Issue 6 / December 2002
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1333-1359
- Print publication:
- December 2002
-
- Article
- Export citation
Half-eigenvalues of elliptic operators
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 132 / Issue 6 / December 2002
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1439-1451
- Print publication:
- December 2002
-
- Article
- Export citation
A finitely generated variety of combinatorial inverse semigroups having uncountably many subvarieties
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 132 / Issue 6 / December 2002
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1373-1394
- Print publication:
- December 2002
-
- Article
- Export citation
Nonlinear eigenvalue–eigenvector problems for STP matrices
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 132 / Issue 6 / December 2002
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1307-1331
- Print publication:
- December 2002
-
- Article
- Export citation
Schauder estimates for fully nonlinear elliptic difference operators
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 132 / Issue 6 / December 2002
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1395-1406
- Print publication:
- December 2002
-
- Article
- Export citation
Existence and decay rates of smooth solutions for a non-uniformly parabolic equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 132 / Issue 6 / December 2002
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1477-1491
- Print publication:
- December 2002
-
- Article
- Export citation
Semilinear elliptic boundary-value problems in combustion theory*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 132 / Issue 6 / December 2002
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1453-1476
- Print publication:
- December 2002
-
- Article
- Export citation
Almost-periodic solutions of elliptic and parabolic equations in unbounded domains
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 132 / Issue 6 / December 2002
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1275-1306
- Print publication:
- December 2002
-
- Article
- Export citation
Relaxation and attainment results for an integral functional with unbounded energy well
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 132 / Issue 6 / December 2002
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1513-1523
- Print publication:
- December 2002
-
- Article
- Export citation
Solvable structures and their application to a class of Cauchy problem
-
- Journal:
- European Journal of Applied Mathematics / Volume 13 / Issue 5 / October 2002
- Published online by Cambridge University Press:
- 28 November 2002, pp. 449-477
-
- Article
- Export citation
Concentrically layered energy equilibria of the di-block copolymer problem
-
- Journal:
- European Journal of Applied Mathematics / Volume 13 / Issue 5 / October 2002
- Published online by Cambridge University Press:
- 28 November 2002, pp. 479-496
-
- Article
- Export citation
Direct construction method for conservation laws of partial differential equations Part I: Examples of conservation law classifications
-
- Journal:
- European Journal of Applied Mathematics / Volume 13 / Issue 5 / October 2002
- Published online by Cambridge University Press:
- 28 November 2002, pp. 545-566
-
- Article
- Export citation
Two terms in the lower bound for the superheating field in a semi-infinite film in the weak-κ limit
-
- Journal:
- European Journal of Applied Mathematics / Volume 13 / Issue 5 / October 2002
- Published online by Cambridge University Press:
- 28 November 2002, pp. 517-544
-
- Article
- Export citation
Dynamics of the interface between two immiscible liquids with nearly equal densities under gravity
-
- Journal:
- European Journal of Applied Mathematics / Volume 13 / Issue 5 / October 2002
- Published online by Cambridge University Press:
- 28 November 2002, pp. 497-516
-
- Article
- Export citation
The Wiener Index of Random Trees
-
- Journal:
- Combinatorics, Probability and Computing / Volume 11 / Issue 6 / November 2002
- Published online by Cambridge University Press:
- 21 November 2002, pp. 587-597
-
- Article
- Export citation
Triangle-Freeness is Hard to Detect
-
- Journal:
- Combinatorics, Probability and Computing / Volume 11 / Issue 6 / November 2002
- Published online by Cambridge University Press:
- 21 November 2002, pp. 549-569
-
- Article
- Export citation
Information Loss in Top to Random Shuffling
-
- Journal:
- Combinatorics, Probability and Computing / Volume 11 / Issue 6 / November 2002
- Published online by Cambridge University Press:
- 21 November 2002, pp. 607-627
-
- Article
- Export citation