Refine search
Actions for selected content:
25820 results in Abstract analysis
On Hankel convolutors on certain Hankel transformable function spaces
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 351-369
- Print publication:
- September 1997
-
- Article
-
- You have access
- Export citation
On commutative Noetherian rings which satisfy the radical formula
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 285-293
- Print publication:
- September 1997
-
- Article
-
- You have access
- Export citation
GMJ volume 39 issue 3 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f7
- Print publication:
- September 1997
-
- Article
-
- You have access
- Export citation
Moufang affine buildings have Moufang spherical buildings at infinity
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 237-241
- Print publication:
- September 1997
-
- Article
-
- You have access
- Export citation
Crossing Numbers and Hard Erdős Problems in Discrete Geometry
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 September 1997, pp. 353-358
-
- Article
- Export citation
Limit Laws for the Optimal Directed Tree with Random Costs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 September 1997, pp. 315-335
-
- Article
- Export citation
Inequalities for the maximal eigenvalue of a nonnegative matrix
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 276-284
- Print publication:
- September 1997
-
- Article
-
- You have access
- Export citation
Triangle Factors in Random Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 September 1997, pp. 337-347
-
- Article
- Export citation
Bilinear forms on vector Hardy spaces
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 371-378
- Print publication:
- September 1997
-
- Article
-
- You have access
- Export citation
On product k-Chen submanifolds
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 243-249
- Print publication:
- September 1997
-
- Article
-
- You have access
- Export citation
Log-Concavity and the Spectral Gap of Stochastic Matrices
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 September 1997, pp. 371-379
-
- Article
- Export citation
Square integrable highest weight representations
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 296-321
- Print publication:
- September 1997
-
- Article
-
- You have access
- Export citation
Hamiltonian Cycles Avoiding Prescribed Arcs in Tournaments
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 September 1997, pp. 255-261
-
- Article
- Export citation
Automatic continuity of certain isomorphisms between regular Banach function algebras
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 333-343
- Print publication:
- September 1997
-
- Article
-
- You have access
- Export citation
On Medians of Lattice Distributions and a Game with Two Dice
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 September 1997, pp. 273-294
-
- Article
- Export citation
Tied Favourite Edges for Simple Random Walk
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 September 1997, pp. 359-369
-
- Article
- Export citation
New Bounds on the List-Chromatic Index of the Complete Graph and Other Simple Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 September 1997, pp. 295-313
-
- Article
- Export citation
Montel subspaces of Fréchet spaces of Moscatelli type
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 345-350
- Print publication:
- September 1997
-
- Article
-
- You have access
- Export citation
A nonlocal problem arising from heat radiation on non-convex surfaces
-
- Journal:
- European Journal of Applied Mathematics / Volume 8 / Issue 4 / August 1997
- Published online by Cambridge University Press:
- 01 August 1997, pp. 403-416
-
- Article
- Export citation
On the minimizers of the Ginzburg–Landau energy for high kappa: the one-dimensional case
-
- Journal:
- European Journal of Applied Mathematics / Volume 8 / Issue 4 / August 1997
- Published online by Cambridge University Press:
- 01 August 1997, pp. 331-345
-
- Article
- Export citation
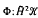 ℋ →
ℋ → 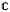 be a bilinear form on vector Hardy space. Introduce the symbol φ of Φ by (φ (
be a bilinear form on vector Hardy space. Introduce the symbol φ of Φ by (φ (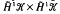 provided that the gradient
provided that the gradient 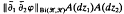 defines a Carleson measure in the bidisc
defines a Carleson measure in the bidisc 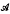 -submanifold (Chen submanifold) to an
-submanifold (Chen submanifold) to an 