Refine search
Actions for selected content:
25820 results in Abstract analysis
The number of blocks with a given defect group
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 2 / December 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 368-373
- Print publication:
- December 1997
-
- Article
- Export citation
An Average-Case Analysis of the Gaussian Algorithm for Lattice Reduction
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 01 December 1997, pp. 397-433
-
- Article
- Export citation
A note on the separation of slow viscous flow near a sharp edge
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 2 / December 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 239-244
- Print publication:
- December 1997
-
- Article
- Export citation
Recovering Set Systems and Graph Entropy
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 01 December 1997, pp. 481-491
-
- Article
- Export citation
The stability of the Strokes layer in periodic orbital flow around a circular cylinder
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 2 / December 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 225-238
- Print publication:
- December 1997
-
- Article
- Export citation
Strong shift equivalence of 2 by 2 non-negative integral matrices
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 2 / December 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 302-312
- Print publication:
- December 1997
-
- Article
- Export citation
Maximal Spacing Configurations in Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 01 December 1997, pp. 455-463
-
- Article
- Export citation
Radial variation of functions in Dirichlet-type spaces
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 2 / December 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 267-277
- Print publication:
- December 1997
-
- Article
- Export citation
The light fluid loading limit for fluid/solid interactions
-
- Journal:
- European Journal of Applied Mathematics / Volume 8 / Issue 5 / October 1997
- Published online by Cambridge University Press:
- 01 October 1997, pp. 485-505
-
- Article
- Export citation
Analysis of thermostat models
-
- Journal:
- European Journal of Applied Mathematics / Volume 8 / Issue 5 / October 1997
- Published online by Cambridge University Press:
- 01 October 1997, pp. 437-455
-
- Article
- Export citation
Source-type solutions to thin-film equations in higher dimensions
-
- Journal:
- European Journal of Applied Mathematics / Volume 8 / Issue 5 / October 1997
- Published online by Cambridge University Press:
- 01 October 1997, pp. 507-524
-
- Article
- Export citation
Critical exponent in a Stefan problem with kinetic condition
-
- Journal:
- European Journal of Applied Mathematics / Volume 8 / Issue 5 / October 1997
- Published online by Cambridge University Press:
- 01 October 1997, pp. 525-532
-
- Article
- Export citation
The influence of material non-uniformity preceding shear-band formation in a model for granular flow
-
- Journal:
- European Journal of Applied Mathematics / Volume 8 / Issue 5 / October 1997
- Published online by Cambridge University Press:
- 01 October 1997, pp. 457-483
-
- Article
- Export citation
Bipartite Coverings of Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 September 1997, pp. 349-352
-
- Article
- Export citation
A note on the punctured neighbourhood theorem
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 269-273
- Print publication:
- September 1997
-
- Article
-
- You have access
- Export citation
The efficiency of PSL(2, p)3 and other direct products of groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 259-268
- Print publication:
- September 1997
-
- Article
-
- You have access
- Export citation
Dependent Sets of Constant Weight Binary Vectors
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 September 1997, pp. 263-271
-
- Article
- Export citation
On the complexity of computing the 2-Selmer group of an elliptic curve
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 251-257
- Print publication:
- September 1997
-
- Article
-
- You have access
- Export citation
Quadratic algebras with few relations
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 323-332
- Print publication:
- September 1997
-
- Article
-
- You have access
- Export citation
GMJ volume 39 issue 3 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- September 1997
-
- Article
-
- You have access
- Export citation
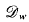 to denote the Dirichlettype space of functions
to denote the Dirichlettype space of functions 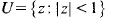 and for which
and for which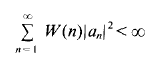
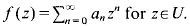 If
If 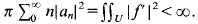 Note also that
Note also that 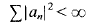 for every
for every 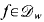 so, by Fatu's theoreum, every function in
so, by Fatu's theoreum, every function in 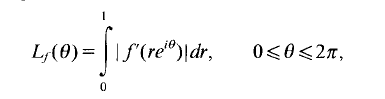
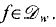
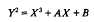
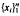 be a basis of
be a basis of 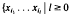 and 1 ≤
and 1 ≤ 