Refine search
Actions for selected content:
25819 results in Abstract analysis
Covering convex bodies by translates of convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 215-218
- Print publication:
- June 1997
-
- Article
- Export citation
On the fractional dimension of sets of continued fractions
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 50-53
- Print publication:
- June 1997
-
- Article
- Export citation
A continuum theory for smectic liquid crystals allowing layer dilation and compression
-
- Journal:
- European Journal of Applied Mathematics / Volume 8 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 01 June 1997, pp. 273-280
-
- Article
- Export citation
M. Aschbacher. 3-Transposition Groups. Cambridge Tracts in Mathematics No. 124. Cambridge University Press. 1997, ISBN 0 521 57196 0, 260 pp., hardback, £35. - S. Axler. Linear Algebra done right. Springer. 1995, ISBN 0 387 94596 2, 238 pp. paperback, DM 40. - E. D. Bloch. A first course in Geometric Topology and Differential Geometry. Birkhäuser. 1997, ISBN 3 7643 3840 7, 421 pp., SFr 98. - J. F. Carlson. Modules and Group Algebras. Birkhäuser. 1996, ISBN 3 7643 5389 9, 91 pp., DM 34. - R. Carter, G. Segal and I. Macdonald. Lectures on Lie Groups and Lie Algebras. LMS Student Texts 32. Cambridge University Press. 1995, ISBN 0 521 49922 4, 190 pp., paperback, £13·95. - J. W. S. Cassels and E. V. Flynn. Prolegomina to a Middle-brow Arithmetic of Curves of Genus 2. Cambridge University Press. 1996, ISBN 0 521 48370 0, 219 pp., paperback, £24·95. - B. Fornberg. A Practical Guide to Pseudospectral Methods. Cambridge Monographs on Applied and Computational Mathematics. Cambridge University Press. 1996, ISBN 0 521 49582 2, 231 pp., £37·50. - B. V. Gnedenko and V. Y. Korolev. Random Summation: Limit Theorems and Applications. CRC Press. 1996, ISBN 0 8493 2875 6, 267 pp., $79.95. - I. Gratton Guinness. The Fontana History of the Mathematical Sciences. Fontana Press. 1997, ISBN 0 00 686179 2, 817 pp., paperback, £12·99. - E. Hernández and G. Weiss. A first course on Wavelets. CRC Press. 1996, ISBN 0 8493 8274 2, 489 pp., $64.95. - N. H. Ibragimov. Editor. Lie group analysis of differential equations. Vol. 3. New Trends in Theoretical Developments and Computational Methods. CRC Press. 1996, ISBN 0 8493 9419 8, 536 pp., $95. - T. W. Körner. The Pleasures of counting. Cambridge University Press. 1996, ISBN 0 521 56823 4, 534 pp., paperback, £17·95. - M. Machover. Set Theory, Logic and their Limitations. Cambridge University Press. 1996, ISBN 0 521 47998 3, 288 pp., paperback, £14·95. - I. Madsen and J. Tornehave. From Calculus to Cohomology. Cambridge University Press. 1997, ISBN 0 521 58956 8, 8, pp. paperback, £16·95. - C. Moeglin and J.-L. Waldspurger. Spectral Decomposition and Eisenstein Series. Cambridge University Press. 1995, ISBN 0 521 41893 3, 338 pp., £50. - C. E. Praeger and L. H. Soicher. Low Rank Representations and Graphs for Sporadic Groups. Australian Math. Soc. Lecture Series, No. 8. Cambridge University Press. 1997, ISBN 0 521 56737 8, 541 pp., paperback, £24·95. - D. Quinney and R. Harding. Calculus Connections, Vol. 1, A Multimedia Adventure. Wiley. 1996, Workbook ISBN 0 471 02111 3, 120 pp., and CD ISBN 0 471 01040, Workbook and CD, £22·50. - L. T. Rigatelli. Evariste Galois, 1811–1832. Birkhäuser. 1996, ISBN 0 8176 5410 0, 163, pp., paperback, SFr 32. - P. G. Saffman. Vortex Dynamics. Cambridge University Press. Reprinted 1995, ISBN 0 521 47739 5, 311 pp., paperback, £17·95. - A. D. Taylor. Mathematics and Politics, Strategy, voting, power and proof. Springer. 1995, ISBN 0 387 94391 9, 284 pp., paperback, £16. - G. Tenenbaum. Introduction to Analytic and Probabilistic Number Theory. Cambridge University Press. 1995, ISBN 0 521 41261 7, 448 pp., £45. - A. van der Poorten. Notes on Fermat's Last Theorem. Wiley. 1996, ISBN 0 471 06261 8, 222 pp., £35. - P. Wojtaszczyk. A mathematical introduction to Wavelets. Cambridge University Press. 1997, ISBN 0 521 57894 9, 261 pp., paperback, £13·95.
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 219-224
- Print publication:
- June 1997
-
- Article
- Export citation
Some Diophantine equations with almost all solutions trivial
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 14-36
- Print publication:
- June 1997
-
- Article
- Export citation
On gaps between numbers that are sums of three cubes
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-13
- Print publication:
- June 1997
-
- Article
- Export citation
On discrepancy bounds via dual shatter function
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 42-49
- Print publication:
- June 1997
-
- Article
- Export citation
Editorial. Mathematical models of liquid crystals
-
- Journal:
- European Journal of Applied Mathematics / Volume 8 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 01 June 1997, pp. 251-252
-
- Article
-
- You have access
- Export citation
MTK volume 44 issue 1 Cover and Front matter
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation
Stochastic Analysis of Convergence via Dynamic Representation for a Class of Line-search Algorithms
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 June 1997, pp. 205-229
-
- Article
- Export citation
4 - The principal and dual graphs
-
- Book:
- Introduction to Subfactors
- Published online:
- 21 October 2009
- Print publication:
- 15 May 1997, pp 47-64
-
- Chapter
- Export citation
Contents
-
- Book:
- Introduction to Subfactors
- Published online:
- 21 October 2009
- Print publication:
- 15 May 1997, pp vii-viii
-
- Chapter
- Export citation
2 - Subfactors and index
-
- Book:
- Introduction to Subfactors
- Published online:
- 21 October 2009
- Print publication:
- 15 May 1997, pp 19-32
-
- Chapter
- Export citation
5 - Commuting squares
-
- Book:
- Introduction to Subfactors
- Published online:
- 21 October 2009
- Print publication:
- 15 May 1997, pp 65-100
-
- Chapter
- Export citation
Bibliography
-
- Book:
- Introduction to Subfactors
- Published online:
- 21 October 2009
- Print publication:
- 15 May 1997, pp 151-155
-
- Chapter
- Export citation
Bibliographical Remarks
-
- Book:
- Introduction to Subfactors
- Published online:
- 21 October 2009
- Print publication:
- 15 May 1997, pp 156-159
-
- Chapter
- Export citation
Appendix
-
- Book:
- Introduction to Subfactors
- Published online:
- 21 October 2009
- Print publication:
- 15 May 1997, pp 133-150
-
- Chapter
- Export citation
Acknowledgement
-
- Book:
- Introduction to Subfactors
- Published online:
- 21 October 2009
- Print publication:
- 15 May 1997, pp xii-xii
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Introduction to Subfactors
- Published online:
- 21 October 2009
- Print publication:
- 15 May 1997, pp i-vi
-
- Chapter
- Export citation
3 - Some basic facts
-
- Book:
- Introduction to Subfactors
- Published online:
- 21 October 2009
- Print publication:
- 15 May 1997, pp 33-46
-
- Chapter
- Export citation
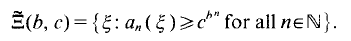
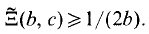 On the other hand, Moorthy [8] showed that dim
On the other hand, Moorthy [8] showed that dim 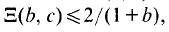 where
where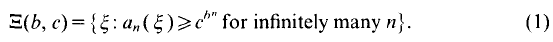
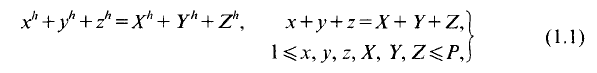

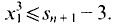 Then
Then 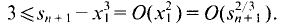 This procedure is iterated by choosing
This procedure is iterated by choosing 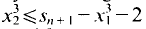 and
and 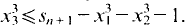 Thus
Thus 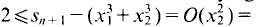
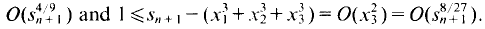 Since
Since 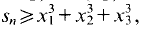 this implies (1).
this implies (1).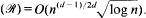 We prove that for
We prove that for 