Let ν be a valuation of any rank of a field K with value group Gν and f(X)= Xm + alXm−1 + … + am be a polynomial over K. In this paper, it is shown that if (ν(ai)/i)≥(ν(am)/m)>0 for l≤i≤m, and there does not exist any integer r>1 dividing m such that ν(am)/r∈Gν, then f(X) is irreducible over K. It is derived as a special case of a more general result proved here. It generalizes the usual Eisenstein Irreducibility Criterion and an Irreducibility Criterion due to Popescu and Zaharescu for discrete, rank-1 valued fields, (cf. [Journal of Number Theory, 52 (1995), 98–118]).

Recently Edelman and Reiner suggested two poset structures, (n, d) and (n, d) on the set of all triangulations of the cyclic d-polytope C(n, d) with n vertices. Both posets are generalizations of the well-studied Tamari lattice. While (n, d) is bounded by definition, the same is not obvious for (n, d). In the paper by Edelman and Reiner the bounds of (n, d) were also confirmed for (n, d) whenever d≤5, leaving the general case as a conjecture.

A model for Poiseuille flow of nematic liquid crystals is examined where a layered structure of defects parallel to the flow is present. Constant gradient flows are discussed, together with symmetric and chevron configurations for such flow problems.

In this paper we consider the Markov process defined by

P1,1=1, Pn,[lscr]=(1−λn,[lscr])·Pn−1,[lscr]+λn,[lscr]−1·Pn−1,[lscr]−1

for transition probabilities λn,[lscr]=q[lscr] and λn,[lscr]=qn−1. We give closed forms for the distributions and the moments of the underlying random variables. Thereby we observe that the distributions can be easily described in terms of q-Stirling numbers of the second kind. Their occurrence in a purely time dependent Markov process allows a natural approximation for these numbers through the normal distribution. We also show that these Markov processes describe some parameters related to the study of random graphs as well as to the analysis of algorithms.

Let M be a compact flat Riemannian manifold of dimension n, and Γ its fundamental group. Then we have the following exact sequence (see [1])

where Zn is a maximal abelian subgroup of Γ and G is a finite group isomorphic to the holonomy group of M. We shall call Γ a Bieberbach group. Let T be a flat torus, and let Ggr act via isometries on T; then ┌ acts isometrically on × T where is the universal covering of M and yields a flat Riemannian structure on ( × T)/Γ. A flat-toral extension (see [9, p. 371]) of the Riemannian manifold M is any Riemannian manifold isometric to ( × T)/Γ where T is a flat torus on which Γ acts via isometries. It is convenient to adopt the convention that a single point is a 0-dimensional flat torus. If this is done, M is itself among the flat toral extensions of M. Roughly speaking, this is a way of putting together a compact flat manifold and a flat torus to make a new flat manifold the dimension of which is the sum of the dimensions of its constituents. It is, more precisely, a fibre bundle over the flat manifold with a flat torus as fibre.

In generalisation of the beta law obtained under the GEM/Poisson–Dirichlet distribution in Hirth [12] we undertake here an analogous construction which results in the Dirichlet law. Our proof makes use of Hoppe's Pólya-like urn model in population genetics.

In what follows, R will denote a commutative domain with 1, and Q(≠R) its field of quotients, which is viewed here as an R-module. By RP we denote the localization of R at the maximal ideal P, and more generally, by MP = Rp⊗RM the localization of the R-module M at P, which we define to be the P-component of M. The symbol R* will mean the multiplicative monoid of nonzero elements of R. For a submonoid S of R*, Rs will denote the localization of R at S.

We review the main outcomes of a continuum theory for the equilibrium of the interface between a nematic liquid crystal and an isotropic environment, in which the surface free energy density bears terms linear in the principal curvatures of the interface. Such geometric contributions to the energy occur together with more conventional elastic contribution, leading to an effective azimuthal anchoring of the optic axis, which breaks the isotropic symmetry of the interface. The theory assumes the interface to be fixed, as for a rigid cavity filled with liquid crystal, and so it does not apply to drops. It should be appropriate when the curvatures of the interface are small compared to that of the molecular interaction sphere. Also, interfaces bearing a sharp edge are encompassed within the theory; a line integral expresses the energy condensed along the edge: we see how it affects the equilibrium equations.

It is proved that the smallest cardinality among the maximal irredundant sets in an n–vertex graph with maximum degree Δ([ges ]2) is at least 2n/3Δ. This substantially improves a bound by Bollobás and Cockayne [1]. The class of graphs which attain this bound is characterised.

An intersecting system of type (∃, ∀, k, n) is a collection []={[Fscr]1, ...,[Fscr]m} of pairwise disjoint families of k-subsets of an n-element set satisfying the following condition. For every ordered pair [Fscr]i and [Fscr]j of distinct members of [] there exists an A∈[Fscr]i that intersects every B∈[Fscr]j. Let In(∃, ∀, k) denote the maximum possible cardinality of an intersecting system of type (∃, ∀, k, n). Ahlswede, Cai and Zhang conjectured that for every k≥1, there exists an n0(k) so that In(∃, ∀, k)=(n−1/k−1) for all n>n0(k). Here we show that this is true for k≤3, but false for all k≥8. We also prove some related results.

Call a set of natural numbers subset-sum-distinct (or SSD) if all pairwise distinct subsets have unequal sums. One wants to construct SSD sets in which the largest element is as small as possible. Given any SSD set, it is easy to construct an SSD set with one more element in which the biggest element is exactly double the biggest element in the original set. For any SSD set, we construct another SSD set with k more elements whose largest element is less than 2k times the largest element in the original set. This claim has been made previously for a different construction, but we show that that claim is false.

We consider a chiral smectic C liquid crystal confined between parallel plates in the bookshelf geometry. Using a recently proposed continuum theory for such materials the behaviour of the cell is discussed when an electric field is applied and subsequently removed from the cell. We examine both symmetric and asymmetric boundary conditions for the director.

Decompositions of simply connected 4-manifolds into three closed 4-balls are studied from the view-point of abstract regular polytopes of Schläfli type {p, q, 2, 3}. The three balls correspond to three ditopes, their common intersection corresponds to a regular map of type {p, q} as an equilibrium surface whose genus equals the “genus” of the 4-manifold.

A sharper form of the Szarek–Talagrand ‘isomorphic’ version of the Sauer–Shelah lemma is proved. Also we prove an analogous ‘isomorphic’ version of the Karpovsky–Milman lemma, which is a generalization of that due to Sauer and Shelah.

It has been known for several years that the lattice of subspaces of a finite vector space has a decomposition into symmetric chains, i.e. a decomposition into disjoint chains that are symmetric with respect to the rank function of the lattice. This paper gives a positive answer to the long-standing open problem of providing an explicit construction of such a symmetric chain decomposition for a given lattice of subspaces of a finite (dimensional) vector space. The construction is done inductively using Schubert normal forms and results in a bracketing algorithm similar to the well-known algorithm for Boolean lattices.

This paper is concerned with the analysis of locally time-synchronized slot systems for broadcast in packet radio networks. Local synchronization has been proposed in practice as less expensive than global synchronization over very wide areas, or over mobile networks. In the case of two locally coordinated groups of stations, under the assumption that the phase shift on the clocks between the two groups is random, it is shown that the probability of no collision is maximized when occupied slots within each group are chosen consecutively, regardless of the number of total slots, or the number of occupied slots in either group.

In this note we point out that a simple proof of the lower bound of the sets (b, c), and so also of Ξ(b, c), defined in the previous paper [1] can be obtained as a simple application of a general method. By Example 4.6 from [2], if [0, 1] = E0⊃E1⊃ … are sets each of which is a finite union of disjoint closed intervals such that each interval of Ek−1, contains at least mk intervals of Ek which are separated by gaps of lengths at least εk, and if mk≥2 and εk≥εk+1>0, then the dimension of the intersection of Ek is at least

We introduce a class of “differential operators” on graphs and we prove an energy estimate and a Liouville type theorem depending on some structural properties of the operators considered.

We explore the ‘Hausdorff dimension at infinity’ for self-affine carpets defined on the square lattice. This notion of dimension (due to Barlow and Taylor), which is the correct notion from a probabilistic perspective, differs for these sets from more ‘naive’ indices of fractal dimension.

We provide a unified and simplified proof that for any partition of (0, 1] into sets that are measurable or have the property of Baire, one cell will contain an infinite sequence together with all of its sums (finite or infinite) without repetition. In fact any set which is large around 0 in the sense of measure or category will contain such a sequence. We show that sets with 0 as a density point have very rich structure. 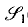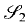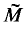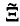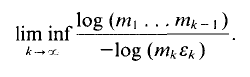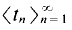Call a sequence and its resulting all-sums set 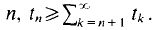structured provided for each We show further that structured all-sums sets with positive measure are not partition regular even if one allows shifted all-sums sets. That is, we produce a two cell measurable partition of (0, 1 ] such that neither set contains a translate of any structured all-sums set with positive measure.