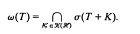Refine search
Actions for selected content:
25819 results in Abstract analysis
1 - Factors
-
- Book:
- Introduction to Subfactors
- Published online:
- 21 October 2009
- Print publication:
- 15 May 1997, pp 1-18
-
- Chapter
- Export citation
Index
-
- Book:
- Introduction to Subfactors
- Published online:
- 21 October 2009
- Print publication:
- 15 May 1997, pp 160-162
-
- Chapter
- Export citation
6 - Vertex and spin models
-
- Book:
- Introduction to Subfactors
- Published online:
- 21 October 2009
- Print publication:
- 15 May 1997, pp 101-132
-
- Chapter
- Export citation
Preface
-
- Book:
- Introduction to Subfactors
- Published online:
- 21 October 2009
- Print publication:
- 15 May 1997, pp ix-xi
-
- Chapter
- Export citation
On the distribution of αpk modulo 1
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 2 / May 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 121-130
- Print publication:
- May 1997
-
- Article
-
- You have access
- Export citation
GMJ volume 39 issue 2 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 2 / May 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- May 1997
-
- Article
-
- You have access
- Export citation
Mixed Hilbert modular forms and families of abelian varieties
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 2 / May 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 131-140
- Print publication:
- May 1997
-
- Article
-
- You have access
- Export citation
The modulus of near smoothness of the lp product of a sequence of Banach spaces
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 2 / May 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 153-165
- Print publication:
- May 1997
-
- Article
-
- You have access
- Export citation
A note on the theorem of Jarník-Besicovitch
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 2 / May 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 233-236
- Print publication:
- May 1997
-
- Article
-
- You have access
- Export citation
An estimate on the eigenvalues in bifurcation for gradient mappings
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 2 / May 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 211-216
- Print publication:
- May 1997
-
- Article
-
- You have access
- Export citation
A family of conformally asymmetric Riemann surfaces
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 2 / May 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 221-225
- Print publication:
- May 1997
-
- Article
-
- You have access
- Export citation
Matched pairs of Lie algebroids
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 2 / May 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 167-181
- Print publication:
- May 1997
-
- Article
-
- You have access
- Export citation
Basis of quadratic differentials for Riemann surfaces with automorphisms
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 2 / May 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 193-210
- Print publication:
- May 1997
-
- Article
-
- You have access
- Export citation
GMJ volume 39 issue 2 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 2 / May 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- May 1997
-
- Article
-
- You have access
- Export citation
Two exponential Diophantine equations
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 2 / May 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 231-232
- Print publication:
- May 1997
-
- Article
-
- You have access
- Export citation
Pietsch integral operators defined on injective tensor products of spaces and applications
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 2 / May 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 227-230
- Print publication:
- May 1997
-
- Article
-
- You have access
- Export citation
Measurable majorants in L1
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 2 / May 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 183-192
- Print publication:
- May 1997
-
- Article
-
- You have access
- Export citation
Groups with few non-nilpotent subgroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 2 / May 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 141-151
- Print publication:
- May 1997
-
- Article
-
- You have access
- Export citation
Weyl's theorem holds for p-hyponormal operators*
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 2 / May 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 217-220
- Print publication:
- May 1997
-
- Article
-
- You have access
- Export citation
Fibre-streamline flows of fibre-reinforced viscous fluids
-
- Journal:
- European Journal of Applied Mathematics / Volume 8 / Issue 2 / April 1997
- Published online by Cambridge University Press:
- 01 April 1997, pp. 209-215
-
- Article
- Export citation

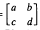 and χ(
and χ(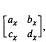 , where
, where 
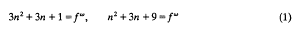

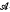 -measurability is that of the conditional expectation
-measurability is that of the conditional expectation 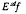 throughout the remainder of this note. Two properties of conditional expectation that may be exploited to gain information, but which also limit conditional expectation's use are the following.
throughout the remainder of this note. Two properties of conditional expectation that may be exploited to gain information, but which also limit conditional expectation's use are the following.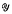 of ℋ, the norm closure of
of ℋ, the norm closure of 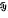 . The Weyl spectrum ω(
. The Weyl spectrum ω(