Refine search
Actions for selected content:
25819 results in Abstract analysis
Global well-posedness and conservation laws for the water wave interaction equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 2 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 369-384
- Print publication:
- 1997
-
- Article
- Export citation
A note on the diophantine equation x2 + 7 = yn
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 1 / January 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 59-63
- Print publication:
- January 1997
-
- Article
-
- You have access
- Export citation
Regional blow-up of solutions to the initial boundary value problem for ut = uδ(Δu + u)
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 4 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 871-887
- Print publication:
- 1997
-
- Article
- Export citation
Robustness and convergence of suboptimal controls in distributed parameter systems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 6 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1153-1179
- Print publication:
- 1997
-
- Article
- Export citation
Unique continuation properties of the nonlinear Schrödinger equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 1 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 191-205
- Print publication:
- 1997
-
- Article
- Export citation
Inhomogeneous Fuchs equations and the limit cycles in a class of near-integrable quadratic systems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 6 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1207-1217
- Print publication:
- 1997
-
- Article
- Export citation
On the adjoint group of some radical rings
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 1 / January 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 35-41
- Print publication:
- January 1997
-
- Article
-
- You have access
- Export citation
Normal forms for periodic retarded functional differential equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 1 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 21-46
- Print publication:
- 1997
-
- Article
- Export citation
A generic property of the resonance set of an elliptic operator with respect to the domain*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 6 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1301-1310
- Print publication:
- 1997
-
- Article
- Export citation
A note on the representation theory of the Hecke algebra of type F4
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 1 / January 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 43-50
- Print publication:
- January 1997
-
- Article
-
- You have access
- Export citation
PRM volume 127 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 4 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1997
-
- Article
-
- You have access
- Export citation
On non-negative quasiconvex functions with unbounded zero sets
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 2 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 411-422
- Print publication:
- 1997
-
- Article
- Export citation
Sharp uniform bounds for steady potential fluid-Poisson systems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 3 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 479-516
- Print publication:
- 1997
-
- Article
- Export citation
Lowersemicontinuity of energy clusters
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 4 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 819-822
- Print publication:
- 1997
-
- Article
- Export citation
Stochastic systems governed by B-evolutions on Hilbert spaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 5 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 903-920
- Print publication:
- 1997
-
- Article
- Export citation
On the profile of solutions with two sharp layers to a singularly perturbed semilinear Dirichlet problem
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 4 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 691-701
- Print publication:
- 1997
-
- Article
- Export citation
Cauchy problem for the Ginzburg-Landau equation for the superconductivity model
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 6 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1181-1192
- Print publication:
- 1997
-
- Article
- Export citation
GMJ volume 39 issue 1 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 1 / January 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- January 1997
-
- Article
-
- You have access
- Export citation
Travelling fronts in nonlocal models for phase separation in an external field*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 4 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 823-835
- Print publication:
- 1997
-
- Article
- Export citation
Bifurcation from homoclinic to periodic solutions in singularly perturbed differential inclusions
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 4 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 727-753
- Print publication:
- 1997
-
- Article
- Export citation
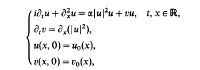
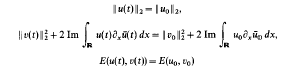
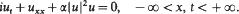
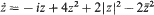 which represents one of two codimension-five components in the intersection of two strata in the centre manifold,
which represents one of two codimension-five components in the intersection of two strata in the centre manifold, 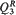 and
and 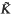 , uniform in the parameter
, uniform in the parameter 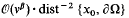 that depends on
that depends on 