Refine search
Actions for selected content:
25816 results in Abstract analysis
The second Hamiltonian structure for the periodic Toda lattice
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 3 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 547-566
- Print publication:
- 1997
-
- Article
- Export citation
Invariant radicals
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 4 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 773-780
- Print publication:
- 1997
-
- Article
- Export citation
First-order corrections to the homogenised eigenvalues of a periodic composite medium. A convergence proof
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 6 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1263-1299
- Print publication:
- 1997
-
- Article
- Export citation
Topological invariants of germs of real analytic functions
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 1 / January 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 85-89
- Print publication:
- January 1997
-
- Article
-
- You have access
- Export citation
Lower semicontinuity in Sobolev spaces below the growth exponent of the integrand
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 4 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 797-817
- Print publication:
- 1997
-
- Article
- Export citation
Optimal existence and uniqueness in a nonlinear diffusion–absorption equation with critical exponents
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 2 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 217-242
- Print publication:
- 1997
-
- Article
- Export citation
On the period maps of projective hypersurfaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 4 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 859-869
- Print publication:
- 1997
-
- Article
- Export citation
Existence and uniqueness of discontinuous solutions for a hyperbolic system
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 6 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1193-1205
- Print publication:
- 1997
-
- Article
- Export citation
On rational de Rham cohomology associated with the generalised confluent hypergeometric functions I, ℙ1 case
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 1 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 145-155
- Print publication:
- 1997
-
- Article
- Export citation
Renormalised solutions of nonlinear parabolic problems with L1 data: existence and uniqueness
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 6 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1137-1152
- Print publication:
- 1997
-
- Article
- Export citation
Young measures in a nonlocal phase transition problem
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 3 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 615-637
- Print publication:
- 1997
-
- Article
- Export citation
Positive definite temperature functions and a correspondence to positive temperature functions
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 5 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 947-961
- Print publication:
- 1997
-
- Article
- Export citation
Index to Volume 127
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 6 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1327-1330
- Print publication:
- 1997
-
- Article
- Export citation
PRM volume 127 issue 3 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 3 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1997
-
- Article
-
- You have access
- Export citation
Eigenvalue problems for the wave equation with strong damping
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 4 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 755-771
- Print publication:
- 1997
-
- Article
- Export citation
On the inhomogeneous system of isentropic gas dynamics by the viscosity method
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 2 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 261-280
- Print publication:
- 1997
-
- Article
- Export citation
Justification of mean-field coupled modulation equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 3 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 639-650
- Print publication:
- 1997
-
- Article
- Export citation
GMJ volume 39 issue 1 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 1 / January 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- January 1997
-
- Article
-
- You have access
- Export citation
On the zeros of the second derivative
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 2 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 359-368
- Print publication:
- 1997
-
- Article
- Export citation
A variational problem on subsets of ℝn
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 127 / Issue 5 / 1997
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1089-1101
- Print publication:
- 1997
-
- Article
- Export citation
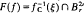 , where 0 ≤ ξ ≪
, where 0 ≤ ξ ≪ 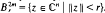 . In [2] Szafraniec introduced the notion of an
. In [2] Szafraniec introduced the notion of an 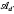 -germ as a generalization of a germ defined by a weighted homogeneous polynomial satisfying some condition concerning the relation between its degree and weights (definition 1). He also proved that if
-germ as a generalization of a germ defined by a weighted homogeneous polynomial satisfying some condition concerning the relation between its degree and weights (definition 1). He also proved that if 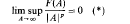
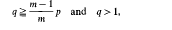
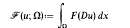
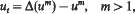
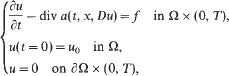
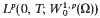 into its dual space. The renormalised solution is an element of
into its dual space. The renormalised solution is an element of 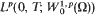 with
with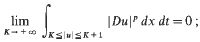
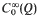 and where
and where 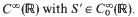
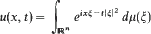
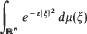
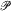 is introduced to give an isomorphism between the class ofall positive definite temperature functions and the class of all possible temperature functions in
is introduced to give an isomorphism between the class ofall positive definite temperature functions and the class of all possible temperature functions in 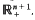 Then correspondence given by
Then correspondence given by 