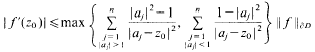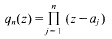Refine search
Actions for selected content:
25819 results in Abstract analysis
Part one - Reachable sets and controllability
-
- Book:
- Geometric Control Theory
- Published online:
- 07 October 2009
- Print publication:
- 28 December 1996, pp 1-2
-
- Chapter
- Export citation
10 - Time-optimal problems and Fuller's phenomenon
-
- Book:
- Geometric Control Theory
- Published online:
- 07 October 2009
- Print publication:
- 28 December 1996, pp 300-331
-
- Chapter
- Export citation
References
-
- Book:
- Geometric Control Theory
- Published online:
- 07 October 2009
- Print publication:
- 28 December 1996, pp 483-488
-
- Chapter
- Export citation
12 - Optimal problems on Lie groups
-
- Book:
- Geometric Control Theory
- Published online:
- 07 October 2009
- Print publication:
- 28 December 1996, pp 368-406
-
- Chapter
- Export citation
5 - Linear and polynomial control systems
-
- Book:
- Geometric Control Theory
- Published online:
- 07 October 2009
- Print publication:
- 28 December 1996, pp 125-149
-
- Chapter
- Export citation
9 - Singular linear quadratic problems
-
- Book:
- Geometric Control Theory
- Published online:
- 07 October 2009
- Print publication:
- 28 December 1996, pp 259-299
-
- Chapter
- Export citation
Part two - Optimal control theory
-
- Book:
- Geometric Control Theory
- Published online:
- 07 October 2009
- Print publication:
- 28 December 1996, pp 195-198
-
- Chapter
- Export citation
Index
-
- Book:
- Geometric Control Theory
- Published online:
- 07 October 2009
- Print publication:
- 28 December 1996, pp 489-492
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Geometric Control Theory
- Published online:
- 07 October 2009
- Print publication:
- 28 December 1996, pp xvii-xviii
-
- Chapter
- Export citation
1 - Basic formalism and typical problems
-
- Book:
- Geometric Control Theory
- Published online:
- 07 October 2009
- Print publication:
- 28 December 1996, pp 3-31
-
- Chapter
- Export citation
2 - Orbits of families of vector fields
-
- Book:
- Geometric Control Theory
- Published online:
- 07 October 2009
- Print publication:
- 28 December 1996, pp 32-63
-
- Chapter
- Export citation
4 - Control affine systems
-
- Book:
- Geometric Control Theory
- Published online:
- 07 October 2009
- Print publication:
- 28 December 1996, pp 95-124
-
- Chapter
- Export citation
Contents
-
- Book:
- Geometric Control Theory
- Published online:
- 07 October 2009
- Print publication:
- 28 December 1996, pp vii-xii
-
- Chapter
- Export citation
13 - Symmetry, integrability, and the Hamilton-Jacobi theory
-
- Book:
- Geometric Control Theory
- Published online:
- 07 October 2009
- Print publication:
- 28 December 1996, pp 407-443
-
- Chapter
- Export citation
Introduction
-
- Book:
- Geometric Control Theory
- Published online:
- 07 October 2009
- Print publication:
- 28 December 1996, pp xiii-xvi
-
- Chapter
- Export citation
6 - Systems on Lie groups and homogeneous spaces
-
- Book:
- Geometric Control Theory
- Published online:
- 07 October 2009
- Print publication:
- 28 December 1996, pp 150-194
-
- Chapter
- Export citation
On the divisor function d(n)
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 320-322
- Print publication:
- December 1996
-
- Article
- Export citation
Sharp extensions of Bernstein's inequality to rational spaces
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 413-423
- Print publication:
- December 1996
-
- Article
- Export citation
Almost Fréchet differentiability of finitely many Lipschitz functions
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 393-412
- Print publication:
- December 1996
-
- Article
- Export citation
A note on summands of compact convex sets
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 286-294
- Print publication:
- December 1996
-
- Article
- Export citation