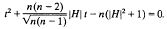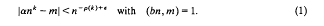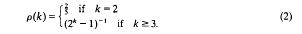Refine search
Actions for selected content:
25816 results in Abstract analysis
V - The fundamental properties of Analytic Functions; Taylor's, Laurent's and Liouville's Theorems
-
- Book:
- A Course of Modern Analysis
- Published online:
- 05 September 2013
- Print publication:
- 13 September 1996, pp 82-110
-
- Chapter
- Export citation
XXII - The Jacobian Elliptic Functions
-
- Book:
- A Course of Modern Analysis
- Published online:
- 05 September 2013
- Print publication:
- 13 September 1996, pp 491-535
-
- Chapter
- Export citation
1 - Analytic Preparations
-
- Book:
- Geometric Applications of Fourier Series and Spherical Harmonics
- Published online:
- 11 September 2009
- Print publication:
- 13 September 1996, pp 1-16
-
- Chapter
- Export citation
Part I - THE PROCESSES OF ANALYSIS
-
- Book:
- A Course of Modern Analysis
- Published online:
- 05 September 2013
- Print publication:
- 13 September 1996, pp 1-2
-
- Chapter
- Export citation
Subject Index
-
- Book:
- Geometric Applications of Fourier Series and Spherical Harmonics
- Published online:
- 11 September 2009
- Print publication:
- 13 September 1996, pp 326-329
-
- Chapter
- Export citation
XIII - The Zeta Function of Riemann
-
- Book:
- A Course of Modern Analysis
- Published online:
- 05 September 2013
- Print publication:
- 13 September 1996, pp 265-280
-
- Chapter
- Export citation
X - Linear Differential Equations
-
- Book:
- A Course of Modern Analysis
- Published online:
- 05 September 2013
- Print publication:
- 13 September 1996, pp 194-210
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- A Course of Modern Analysis
- Published online:
- 05 September 2013
- Print publication:
- 13 September 1996, pp i-iv
-
- Chapter
- Export citation
GENERAL INDEX
-
- Book:
- A Course of Modern Analysis
- Published online:
- 05 September 2013
- Print publication:
- 13 September 1996, pp 595-608
-
- Chapter
- Export citation
4 - Geometric Applications of Fourier Series
-
- Book:
- Geometric Applications of Fourier Series and Spherical Harmonics
- Published online:
- 11 September 2009
- Print publication:
- 13 September 1996, pp 133-180
-
- Chapter
- Export citation
XXI - The Theta Functions
-
- Book:
- A Course of Modern Analysis
- Published online:
- 05 September 2013
- Print publication:
- 13 September 1996, pp 462-490
-
- Chapter
- Export citation
Part II - THE TRANSCENDENTAL FUNCTIONS
-
- Book:
- A Course of Modern Analysis
- Published online:
- 05 September 2013
- Print publication:
- 13 September 1996, pp 233-234
-
- Chapter
- Export citation
III - Continuous Functions and Uniform Convergence
-
- Book:
- A Course of Modern Analysis
- Published online:
- 05 September 2013
- Print publication:
- 13 September 1996, pp 41-60
-
- Chapter
- Export citation
XV - Legendre Functions
-
- Book:
- A Course of Modern Analysis
- Published online:
- 05 September 2013
- Print publication:
- 13 September 1996, pp 302-336
-
- Chapter
- Export citation
Finite groups of outer automorphisms of free groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 275-282
- Print publication:
- September 1996
-
- Article
-
- You have access
- Export citation
Complete submanifolds with parallel mean curvature in a sphere
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 343-346
- Print publication:
- September 1996
-
- Article
-
- You have access
- Export citation
GMJ volume 38 issue 3 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f8
- Print publication:
- September 1996
-
- Article
-
- You have access
- Export citation
A generalized Drazin inverse
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 367-381
- Print publication:
- September 1996
-
- Article
-
- You have access
- Export citation
A class of groups rich in finite quotients
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 263-274
- Print publication:
- September 1996
-
- Article
-
- You have access
- Export citation
A problem of Hooley in Diophantine approximation
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 299-308
- Print publication:
- September 1996
-
- Article
-
- You have access
- Export citation