Refine search
Actions for selected content:
25816 results in Abstract analysis
On a hyperlogistic delay equation
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 2 / May 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 255-261
- Print publication:
- May 1996
-
- Article
-
- You have access
- Export citation
GMJ volume 38 issue 2 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 2 / May 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- May 1996
-
- Article
-
- You have access
- Export citation
A nontrivial T1-space admitting a unique quasi-proximity
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 2 / May 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 207-213
- Print publication:
- May 1996
-
- Article
-
- You have access
- Export citation
A note on comonotonic additivity
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 2 / May 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 199-205
- Print publication:
- May 1996
-
- Article
-
- You have access
- Export citation
A note concerning the ideal of nuclear operators
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 2 / May 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 233-236
- Print publication:
- May 1996
-
- Article
-
- You have access
- Export citation
Automorphic forms on nondiscrete Möbius groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 2 / May 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 249-253
- Print publication:
- May 1996
-
- Article
-
- You have access
- Export citation
Finite co-Dedekindian groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 2 / May 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 163-169
- Print publication:
- May 1996
-
- Article
-
- You have access
- Export citation
On linear recurrence sequences with polynomial coefficients
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 2 / May 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 147-155
- Print publication:
- May 1996
-
- Article
-
- You have access
- Export citation
GMJ volume 38 issue 2 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 2 / May 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- May 1996
-
- Article
-
- You have access
- Export citation
Solutions of Diophantine equations and divisibility of class numbers of complex quadratic fields
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 2 / May 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 196-197
- Print publication:
- May 1996
-
- Article
-
- You have access
- Export citation
Strong bands of groups of left quotients
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 2 / May 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 237-242
- Print publication:
- May 1996
-
- Article
-
- You have access
- Export citation
Models for joint isometries
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 2 / May 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 191-194
- Print publication:
- May 1996
-
- Article
-
- You have access
- Export citation
Boundaries of nonpositively curved groups of the form G × ℤn
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 2 / May 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 177-189
- Print publication:
- May 1996
-
- Article
-
- You have access
- Export citation
On the topological degree of real polynomial vector fields
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 2 / May 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 221-231
- Print publication:
- May 1996
-
- Article
-
- You have access
- Export citation
An extension of the Kegel–Wielandt theorem to locally finite groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 2 / May 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 171-176
- Print publication:
- May 1996
-
- Article
-
- You have access
- Export citation
Some remarks on regular Banach spaces
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 2 / May 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 243-248
- Print publication:
- May 1996
-
- Article
-
- You have access
- Export citation
2 - Pseudoinverses and Tensor Products
-
- Book:
- Neural Networks and Qualitative Physics
- Published online:
- 05 August 2012
- Print publication:
- 29 March 1996, pp 23-43
-
- Chapter
- Export citation
Acknowledgements
-
- Book:
- Neural Networks and Qualitative Physics
- Published online:
- 05 August 2012
- Print publication:
- 29 March 1996, pp xvii-xviii
-
- Chapter
- Export citation
1 - Neural Networks: A Control Approach
-
- Book:
- Neural Networks and Qualitative Physics
- Published online:
- 05 August 2012
- Print publication:
- 29 March 1996, pp 1-22
-
- Chapter
- Export citation
Preface
-
- Book:
- Neural Networks and Qualitative Physics
- Published online:
- 05 August 2012
- Print publication:
- 29 March 1996, pp xi-xvi
-
- Chapter
- Export citation

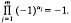 .
.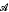 be a Banach algebra of bounded linear operators such that
be a Banach algebra of bounded linear operators such that 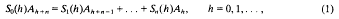
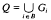 such that
such that 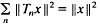 for all
for all 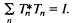 Athavale in [1] characterized the joint isometries as subnormal N-tuples whose minimal normal extensions have joint spectra in the unit sphere
Athavale in [1] characterized the joint isometries as subnormal N-tuples whose minimal normal extensions have joint spectra in the unit sphere 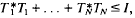 , can be represented as restrictions of certain weighted shifts direct sum a joint isometry. In this paper we adapt the canonical models of [3], and also construct a new canonical model, which completes the previous descriptions by showing joint isometries are indeed restrictions of specific multivariable weighted shifts [2].
, can be represented as restrictions of certain weighted shifts direct sum a joint isometry. In this paper we adapt the canonical models of [3], and also construct a new canonical model, which completes the previous descriptions by showing joint isometries are indeed restrictions of specific multivariable weighted shifts [2].