Refine search
Actions for selected content:
25816 results in Abstract analysis
Cauchy problem for hyperbolic conservation laws with a relaxation term
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 4 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 821-828
- Print publication:
- 1996
-
- Article
- Export citation
Resolution of the spherical piston problem for compressible isentropic gas dynamics via a self-similar viscous limit
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 6 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1309-1340
- Print publication:
- 1996
-
- Article
- Export citation
Commutative orders
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 6 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1201-1216
- Print publication:
- 1996
-
- Article
- Export citation
Multiple positive solutions of nonhomogeneous semilinear elliptic equations in ℝN*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 2 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 443-463
- Print publication:
- 1996
-
- Article
- Export citation
The Penrose–Fife-type equations: counting the one-dimensional stationary solutions
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 3 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 483-504
- Print publication:
- 1996
-
- Article
- Export citation
Heat invariants for odd-dimensional hemispheres
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 1 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 187-193
- Print publication:
- 1996
-
- Article
- Export citation
A systematic study of heteroclinic cycles in dynamical systems with broken symmetries
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 4 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 885-909
- Print publication:
- 1996
-
- Article
- Export citation
On the diophantine equations x2 + 74 = y5 and x2 + 86 = y5
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 1 / January 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 77-85
- Print publication:
- January 1996
-
- Article
-
- You have access
- Export citation
Some remarks on quasiconvexity and rank-one convexity
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 5 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1055-1065
- Print publication:
- 1996
-
- Article
- Export citation
Pseudo-orbit tracing property for random diffeomorphisms*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 5 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1027-1033
- Print publication:
- 1996
-
- Article
- Export citation
A probabilistic approach to blow-up of a semilinear heat equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 6 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1235-1245
- Print publication:
- 1996
-
- Article
- Export citation
A necessary and sufficient condition for finite speed of propagation in the theory of doubly nonlinear degenerate parabolic equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 4 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 739-767
- Print publication:
- 1996
-
- Article
- Export citation
GMJ volume 38 issue 1 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 1 / January 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- January 1996
-
- Article
-
- You have access
- Export citation
The range of non-surjective convolution operators on Beurling spaces
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 1 / January 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 125-135
- Print publication:
- January 1996
-
- Article
-
- You have access
- Export citation
PRM volume 126 issue 3 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 3 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1996
-
- Article
-
- You have access
- Export citation
Sharpness of embeddings in logarithmic Bessel-potential spaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 5 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 995-1009
- Print publication:
- 1996
-
- Article
- Export citation
Multiplicity of homoclinic solutions for singular second-order conservative systems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 6 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1169-1180
- Print publication:
- 1996
-
- Article
- Export citation
Singularly perturbed ordinary differential equations with dynamic limits
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 3 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 541-569
- Print publication:
- 1996
-
- Article
- Export citation
PRM volume 126 issue 5 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 5 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1996
-
- Article
-
- You have access
- Export citation
Linear spaces of real matrices of large rank
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 1 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 147-151
- Print publication:
- 1996
-
- Article
- Export citation
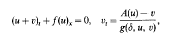
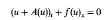
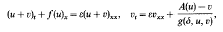
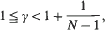
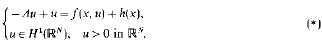
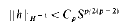
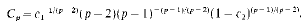
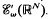 . We investigate the range of the convolution operator
. We investigate the range of the convolution operator 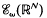 associated with a weight
associated with a weight 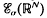 for a weight σ ≥ ω if and only if the convolution operator is surjective on the smaller class.
for a weight σ ≥ ω if and only if the convolution operator is surjective on the smaller class.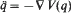 , with
, with 