Refine search
Actions for selected content:
25816 results in Abstract analysis
Open mappings and solvability of nonlinear equations in Banach space
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 2 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 239-246
- Print publication:
- 1996
-
- Article
- Export citation
Disjointly strictly singular operators and interpolation*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 5 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1011-1026
- Print publication:
- 1996
-
- Article
- Export citation
A regularity theorem for minimisers of quasiconvex integrals: the case 1 <p<2*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 6 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1181-1199
- Print publication:
- 1996
-
- Article
- Export citation
Partial and complete linearisations at stationary points of infinite-dimensional dynamical systems with foliations and applications*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 5 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1067-1085
- Print publication:
- 1996
-
- Article
- Export citation
Self-induced compactness in Banach spaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 2 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 355-362
- Print publication:
- 1996
-
- Article
- Export citation
PRM volume 126 issue 1 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 1 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1996
-
- Article
-
- You have access
- Export citation
Practical persistence in ecological models via comparison methods*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 2 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 247-272
- Print publication:
- 1996
-
- Article
- Export citation
Stability and characteristic wavelength of planar interfaces in the large diffusion limit of the inhibitor
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 1 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 117-145
- Print publication:
- 1996
-
- Article
- Export citation
Homogenisation of transport kinetic equations with oscillating potentials
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 6 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1247-1275
- Print publication:
- 1996
-
- Article
- Export citation
Multiscale convergence and reiterated homogenisation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 2 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 297-342
- Print publication:
- 1996
-
- Article
- Export citation
Index to Volume 126
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 6 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1351-1355
- Print publication:
- 1996
-
- Article
- Export citation
Some remarks about relaxation problems in the Calculus of Variations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 3 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 665-675
- Print publication:
- 1996
-
- Article
- Export citation
Singular sets of anisotropic weighted capacity zero and degenerate quasilinear parabolic equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 1 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 209-224
- Print publication:
- 1996
-
- Article
- Export citation
L1-approximation of Fourier series of complex-valued functions
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 2 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 343-353
- Print publication:
- 1996
-
- Article
- Export citation
Equality of essential spectra of quasisimilar operators with property (δ)
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 1 / January 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 21-28
- Print publication:
- January 1996
-
- Article
-
- You have access
- Export citation
A simple proof of Noether's theorem
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 1 / January 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 49-51
- Print publication:
- January 1996
-
- Article
-
- You have access
- Export citation
Cesàro averaging operators on Hardy spaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 3 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 617-624
- Print publication:
- 1996
-
- Article
- Export citation
Long-time behaviour for a model of phase-field type
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 1 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 167-185
- Print publication:
- 1996
-
- Article
- Export citation
The finite Hilbert transform in weighted spaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 6 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1157-1167
- Print publication:
- 1996
-
- Article
- Export citation
A characterisation of tangential exceptional sets for
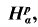 αp = n
αp = n
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 3 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 625-641
- Print publication:
- 1996
-
- Article
- Export citation
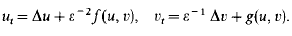
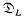 is a free
is a free  -module where Γ=Gal(
-module where Γ=Gal(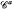 ℜα > – 1, satisfies an inequality which immediately implies that it is bounded on certain Hardy spaces including
ℜα > – 1, satisfies an inequality which immediately implies that it is bounded on certain Hardy spaces including 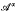 which is conjugate to
which is conjugate to 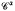 on
on 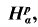 αp = n
αp = n
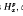 ,
, 