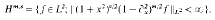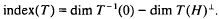Refine search
Actions for selected content:
25816 results in Abstract analysis
The distance function and defect energy
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 5 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 923-938
- Print publication:
- 1996
-
- Article
- Export citation
The 3-local cohomology of the Mathieu group M24
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 1 / January 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 69-75
- Print publication:
- January 1996
-
- Article
-
- You have access
- Export citation
PRM volume 126 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 4 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1996
-
- Article
-
- You have access
- Export citation
PRM volume 126 issue 4 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 4 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1996
-
- Article
-
- You have access
- Export citation
On the convolution operators arising in the study of abstract initial boundary value problems
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 3 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 515-539
- Print publication:
- 1996
-
- Article
- Export citation
On the decay of higher-order norms of the solutions of Navier–Stokes equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 3 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 677-685
- Print publication:
- 1996
-
- Article
- Export citation
On the generators of elementary subgroups of general linear groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 1 / January 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-10
- Print publication:
- January 1996
-
- Article
-
- You have access
- Export citation
Global smooth solution of the nonisentropic gas dynamics system*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 4 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 769-775
- Print publication:
- 1996
-
- Article
- Export citation
Quasidistinguished countable enlargements of normed spaces
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 1 / January 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 65-68
- Print publication:
- January 1996
-
- Article
-
- You have access
- Export citation
Affine length and affine dimension of a 1-set of ℝ2
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 5 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 985-993
- Print publication:
- 1996
-
- Article
- Export citation
An exotic totally real minimal immersion of S3 in ℂP3 and its characterisation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 1 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 153-165
- Print publication:
- 1996
-
- Article
- Export citation
On positive entire solutions of the elliptic equation Δu + K(x)up = 0 and its applications to Riemannian geometry
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 2 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 225-237
- Print publication:
- 1996
-
- Article
- Export citation
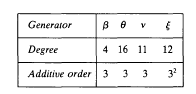
On the algebra of a free monoid
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 5 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 939-945
- Print publication:
- 1996
-
- Article
- Export citation
Semigroup-graded rings with finite support
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 1 / January 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 11-18
- Print publication:
- January 1996
-
- Article
-
- You have access
- Export citation
Dilation method and smoothing effects of solutions to the Benjamin–Ono equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 2 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 273-285
- Print publication:
- 1996
-
- Article
- Export citation
On convexity properties of homogeneous functions of degree one*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 5 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 947-956
- Print publication:
- 1996
-
- Article
- Export citation
A spectral mapping theorem for the Weyl spectrum
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 1 / January 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. 61-64
- Print publication:
- January 1996
-
- Article
-
- You have access
- Export citation
Exponential formulae in quantum stochastic calculus
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 2 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 375-389
- Print publication:
- 1996
-
- Article
- Export citation
GMJ volume 38 issue 1 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 38 / Issue 1 / January 1996
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- January 1996
-
- Article
-
- You have access
- Export citation
The Cauchy problem for the system of Zakharov equations arising from ion-acoustic modes
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 126 / Issue 4 / 1996
- Published online by Cambridge University Press:
- 14 November 2011, pp. 811-820
- Print publication:
- 1996
-
- Article
- Export citation
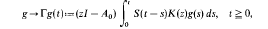
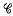 (which includes
(which includes 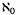 -dimensional subspace of the algebraic dual
-dimensional subspace of the algebraic dual 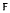 denote a subring of the complex field that contains 1 and is closed under complex conjugation. It is shown that, with respect to the involution induced by word-reversal, the algebra over
denote a subring of the complex field that contains 1 and is closed under complex conjugation. It is shown that, with respect to the involution induced by word-reversal, the algebra over 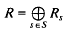 be an
be an 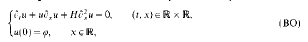
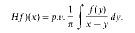
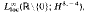 , where
, where