This paper examines the Cauchy problem for a viscoelastic model with relaxation

with discontinuous, large initial data, where ½ ≦ μ <1, δ > 0 are constants. We first give a definition of admissible (or entropic) solutions to the system. Under this definition, we prove the existence, uniqueness and continuous dependence of the global admissible solution for the system. Our methods are essentially due to Kruzkov, and the requirement that f(u) is not badly degenerate (more precisely, meas {x: f″(x) = 0} = 0), needed previously when considering the global existence problem for the same system, is removed.

The asymptotic behaviour for large-time values of solutions of the initial-boundary-value problem for the Benjamin–Bona–Mahony–Burgers (BBMB) equation is studied. The solution of the initial-boundary-value problem is proved to converge to the standing wave as t → ∞ uniformly with respect to x ∈ R1. The estimate obtained of the time-decay rate of the remainder appears to depend on the rate of decay at infinity of the deviation of initial data from the standing wave. Due to the known expansion formulae with respect to the eigenfunctions associated to the stationary Schrodinger operator with the standing wave as a potential, it is possible to find the second term of the large-time asymptotic expansion of the solution to the initial-boundary-value problem for the BBMB equation.

The paper is concerned with the estimation of the number of maximal-length genus n nonorientable Wicks forms for n → ∞. It is shown how to apply a graph theory for this problem. It is proved that if M(n) be the number of all nonequivalent nonorientable genus n Wicks forms of maximal length, then

We study the number and stability of the positive solutions of a reaction–diffusion equation pair. When certain parameters in the equations are large, the equation pair can be viewed as singular or regular perturbations of some single (or essentially single) equation problems, for which the number and stability of their solutions can be well understood. With the help of these simpler equations, we are able to obtain a rather complete understanding of the number and stability of the positive solutions for the equation pair for the cases that certain parameters are large. In particular, we obtain a fairly satisfactory description of the positive solution set of the equation pair.

According to the well-known Nash's theorem, every Riemannian n-manifold admits an isometric immersion into the Euclidean space En(n+1)(3n+11)/2. In general, there exist enormously many isometric immersions from a Riemannian manifold into Euclidean spaces if no restriction on the codimension is made. For a submanifold of a Riemannian manifold there are associated several extrinsic invariants beside its intrinsic invariants. Among the extrinsic invariants, the mean curvature function and shape operator are the most fundamental ones.

It is shown that spectral properties of Sturm–Liouville eigenvalue problems with indefinite weights are related to integral inequalities studied by Everitt. A result of Beals on indefinite problems leads to a sufficient condition for the validity of such an inequality. A Baire category argument is used to show that, in general, the inequality under consideration does not hold.

We prove some results on the global existence of smooth solutions for certain nonlinear parabolic systems of the form Ut + A(U)Ux = DUxx. Here U is a vector and A(U), D are matrices with D a constant, positive matrix. We show how to use our results to study the global continuous (or generalised) solutions to the corresponding nonlinear hyperbolic conservation laws and a conjecture is given.

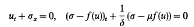
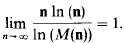
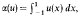Nonlocal reaction–diffusion equations of the form ut = uxx + F(u, α(u)), where are considered together with Neumann or Dirichlet boundary conditions. One of the main results deals with linearisation at equilibria. It states that, for any given set of complex numbers, one can arrange, choosing the equation properly, that this set is contained in the spectrum of the linearisation. The second main result shows that equations of the above form can undergo a supercritical Hopf bifurcation to an asymptotically stable periodic solution.

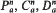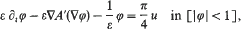
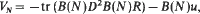
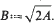First, we establish a sharp inequality between the squared mean curvature and the scalar curvature for a Lagrangian submanifold in a nonflat complex-space-form. Then, by utilising the Jacobi's elliptic functions en and dn, we introduce three families of Lagrangian submanifolds and two exceptional Lagrangian submanifolds Fn, Ln in nonflat complex-space-forms which satisfy the equality case of the inequality. Finally, we obtain the complete classification of Lagrangian submanifolds in nonflat complex-space-forms which satisfy this basic equality.

If Sis a regular semigroup then an inverse transversal of S is an inverse subsemigroup T with the property that |T ∩ V(x)| = 1 for every x ∈ S where V(x) denotes the set of inverses of x ∈ S. In a previous publication [1] we considered the similar concept of a subsemigroup T of S such that |T ∩ A(x)| = 1 for every x ∩ S where A(x) = {y∈ S;xyx = x} denotes the set of associates (or pre-inverses) of x ∈ S, and showed that such a subsemigroup T is necessarily a maximal subgroup Ha for some idempotent α ∈ S. Throughout what follows, we shall assume that S is orthodox and α is a middle unit (in the sense that xαy = xy for all x, y ∈ S). Under these assumptions, we obtained in [1] a structure theorem which generalises that given in [3] for uniquely unit orthodox semigroups. Adopting the notation of [1], we let T ∩ A(x) = {x*} and write the subgroup T as Hα = {x*;x ∈ S}, which we call an associate subgroup of S. For every x ∈ S we therefore have x*α = x* = αx* and x*x** = α = x**x*. As shown in [1, Theorems 4, 5] we also have (xy)* = y*x* for all x, y ∈ S, and e* = α for every idempotent e.

The initial-value problem for the Korteweg-de Vries equation with a forcing term has recently gained prominence as a model for a number of interesting physical situations. At the same time, the modern theory for the initial-value problem for the unforced Korteweg-de Vries equation has taken great strides forward. The mathematical theory pertaining to the forced equation is currently set in narrow function classes and has not kept up with recent advances for the homogeneous equation. This aspect is rectified here with the development of a theory for the initial-value problem for the forced Korteweg-de Vries equation that entails weak assumptions on both the initial wave configuration and the forcing. The results obtained include analytic dependence of solutions on the auxiliary data and allow the external forcing to lie in function classes sufficiently large that a Dirac δ-function or its derivative is included. Analyticity is proved by an infinite-dimensional analogue of Picard iteration. A consequence is that solutions may be approximated arbitrarily well on any bounded time interval by solving a finite number of linear initial-value problems.

We compute the principal term of the asymptotics with a remainder estimate for Schrödinger operators with slowly growing potentials q, a typical example being q(x) = In … In |x| outside some compact.

We study the stability of positive radially symmetric solitary waves for a three dimensional generalisation of the Korteweg de Vries equation, which describes nonlinear ion-acoustic waves in a magnetised plasma, and for a generalisation in dimension two of the Benjamin–Bona–Mahony equation.

In this paper, we prove that solutions of the anisotropic Allen–Cahn equation in doubleobstacle form

where A is a strictly convex function, homogeneous of degree two, converge to an anisotropic mean-curvature flow

when this equation admits a smooth solution in ℝn. Here VN and R respectively denote the normal velocity and the second fundamental form of the interface, and More precisely, we show that the Hausdorff-distance between the zero-level set of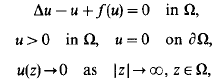 φ and the interface of the above anisotropic mean-curvature flow is of order O(ε2).

In this paper we study the existence of least energy solutions to subcritical semilinear elliptic equations of the form

where Ω is an unbounded domain in RN and f is a C1 function, with appropriate superlinear growth. We state general conditions on the domain Ω so that the associated functional has a nontrivial critical point, thus yielding a solution to the equation. Asymptotic results for domains stretched in one direction are also provided.

We classify multiplicative white noise perturbations k(·) dw, of generalised KPP equations and their effects on deterministic approximate travelling wave solutions by the behaviour of , the solutions of the stochastic generalised KPP equations converge to deterministic approximate travelling waves and if

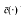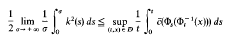
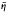being an associated potential energy, Фs a solution of the corresponding classical mechanical equations of Newton, D being a certain domain in R1 × Rr then the white noise perturbations essentially destroy the wave structure and force the solutions to die down.

For the case

(suppose the existence of the limit) we show that there is a residual wave form but propagating at a different speed from that of the unperturbed equations. Numerical solutions are included and give good agreement with theoretical results.

Eigenvalues of both regular and singular Sturm–Liouville (S–L) problems with general coupled self-adjoint boundary conditions are characterised. This characterisation, although elementary, appears to be new even in the regular case. The singular characterisation is an exact parallel of the regular one and reduces to it. One application yields inequalities among the eigenvalues of different coupled boundary conditions. This is a far-reaching extension, even in the regular case, of the well-known relationship among the periodic and semiperiodic eigenvalues.

In this paper we study a nonlocal problem for a second-order partial differential equation which depends on a parameter n. We prove the existence of critical values 0 < and 0 > 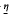such that for all ≦ɳ≦ and for all non-negative right-hand sides, our problem has nonnegative solutions. We obtain a formula for ɳ0, the maximal possible value of , and find the exact value of ɳ for spherical ɳ. We also study the corresponding eigenvalue problem. At the end of the paper, we consider the application of our results to the nonlinear system describing the distribution of temperature and potential in a microsensor.