Refine search
Actions for selected content:
25814 results in Abstract analysis
The transmutation operator for −d2/(w(x) dx2)
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 1 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 85-98
- Print publication:
- 1995
-
- Article
- Export citation
Unbounded solution components for nonlinear Hill's equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 6 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1131-1167
- Print publication:
- 1995
-
- Article
- Export citation
Colour algebras and Cayley–Dickson algebras
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 6 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1287-1303
- Print publication:
- 1995
-
- Article
- Export citation
Symmetric-like Riemannian manifolds and geodesic symmetries
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 2 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 265-282
- Print publication:
- 1995
-
- Article
- Export citation
A reaction-diffusion equation on a thin L-shaped domain
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 2 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 283-327
- Print publication:
- 1995
-
- Article
-
- You have access
- Export citation
Groups of small symmetric genus
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 1 / January 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 115-129
- Print publication:
- January 1995
-
- Article
-
- You have access
- Export citation
Dynamics of a nonlinear convection-diffusion equation in multidimensional bounded domains
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 2 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 439-448
- Print publication:
- 1995
-
- Article
- Export citation
Renormalisation of finitely ramified fractals
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 5 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1085-1104
- Print publication:
- 1995
-
- Article
- Export citation
Trace functions on the algebras of certain E-unitary inverse semigroups
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 5 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1077-1084
- Print publication:
- 1995
-
- Article
- Export citation
Construction of semiabelian Galois extensions
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 1 / January 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 99-104
- Print publication:
- January 1995
-
- Article
-
- You have access
- Export citation
On the eigenvalue asymptotics for a nonselfadjoint elliptic problem involving an indefinite weight
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 4 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 859-875
- Print publication:
- 1995
-
- Article
- Export citation
Variation of constants for hybrid systems of functional differential equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 1 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1-12
- Print publication:
- 1995
-
- Article
- Export citation
Correspondences of completely regular semigroups and
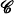 -isomorphisms of semigroups
-isomorphisms of semigroups
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 3 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 625-637
- Print publication:
- 1995
-
- Article
- Export citation
Faithful linear representations of certain free nilpotent groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 1 / January 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 33-36
- Print publication:
- January 1995
-
- Article
-
- You have access
- Export citation
Product submanifolds with pointwise 3-planar normal sections
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 1 / January 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 73-81
- Print publication:
- January 1995
-
- Article
-
- You have access
- Export citation
Instability of quasiperiodic solutions of the Ginzburg–Landau equation
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 3 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 501-517
- Print publication:
- 1995
-
- Article
- Export citation
On semigroups defined by Coxeter-type presentations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 5 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1063-1075
- Print publication:
- 1995
-
- Article
- Export citation
Weak solutions to a hydrodynamic model for semiconductors: the Cauchy problem
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 1 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 115-131
- Print publication:
- 1995
-
- Article
- Export citation
Comparison of complexes of modules of generalized fractions and generalized Hughes complexes
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 1 / January 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 55-64
- Print publication:
- January 1995
-
- Article
-
- You have access
- Export citation
GMJ volume 37 issue 1 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 1 / January 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- January 1995
-
- Article
-
- You have access
- Export citation
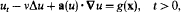
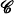 -isomorphisms of semigroups
-isomorphisms of semigroups
 (
(