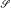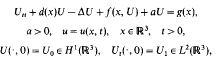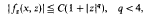Refine search
Actions for selected content:
25814 results in Abstract analysis
PRM volume 125 issue 2 Cover and Front matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 2 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
- Print publication:
- 1995
-
- Article
-
- You have access
- Export citation
The syntactic monoid of the semigroup generated by a comma-free code
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 1 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 165-179
- Print publication:
- 1995
-
- Article
- Export citation
Proximate topology and shape theory
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 3 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 595-615
- Print publication:
- 1995
-
- Article
- Export citation
A symplectic fixed-point theorem for T2k × CPn × CPm
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 3 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 465-492
- Print publication:
- 1995
-
- Article
- Export citation
Boundary value problems on noncompact intervals
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 4 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 777-799
- Print publication:
- 1995
-
- Article
- Export citation
Nilpotents and congruences on semigroups of transformations with fixed rank
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 2 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 399-412
- Print publication:
- 1995
-
- Article
- Export citation
Change of stability for Schrödinger semigroups*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 4 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 827-846
- Print publication:
- 1995
-
- Article
- Export citation
Hilbert modules revisited: orthonormal bases and Hilbert-Schmidt operators
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 1 / January 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 45-54
- Print publication:
- January 1995
-
- Article
-
- You have access
- Export citation
Asymptotic behaviour and attractors for a semilinear damped wave equation with supercritical exponent
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 5 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1051-1062
- Print publication:
- 1995
-
- Article
- Export citation
On the existence of solitary waves in rotating fluids
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 5 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1105-1129
- Print publication:
- 1995
-
- Article
- Export citation
Groups with finitely many conjugacy classes of subgroups with large subnormal defect
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 1 / January 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 69-71
- Print publication:
- January 1995
-
- Article
-
- You have access
- Export citation
Complexity in spatio-temporal dynamics
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 5 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 959-974
- Print publication:
- 1995
-
- Article
- Export citation
High-energy and multi-peaked solutions for a nonlinear Neumann problem with critical exponents*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 5 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1003-1029
- Print publication:
- 1995
-
- Article
- Export citation
PRM volume 125 issue 6 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 6 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1995
-
- Article
-
- You have access
- Export citation
PRM volume 125 issue 4 Cover and Back matter
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 4 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
- Print publication:
- 1995
-
- Article
-
- You have access
- Export citation
Equations for biological evolution*
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 5 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 939-958
- Print publication:
- 1995
-
- Article
- Export citation
On the unitarity of the wave operators for AC-Stark Hamiltonians
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 3 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 617-624
- Print publication:
- 1995
-
- Article
- Export citation
One sided invertibility and localisation II
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 1 / January 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 15-19
- Print publication:
- January 1995
-
- Article
-
- You have access
- Export citation
Periodic orbits of difference equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 4 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 657-674
- Print publication:
- 1995
-
- Article
- Export citation
On commutative idempotent rings
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 125 / Issue 2 / 1995
- Published online by Cambridge University Press:
- 14 November 2011, pp. 341-349
- Print publication:
- 1995
-
- Article
- Export citation