Local models are given for the singularities which can appear on the trajectories of general one-dimensional motions of the plane or space. Versal unfoldings of these model singularities give simple pictures describing the family of trajectories arising from small deformations of the tracing point.

We give a concise approach to generalising the inequalities of Wirtinger, Hardy, Weyl and Opial by using the well-known inequality: if X and Y are non-negative, then

for p > 1 (0 < p < 1), respectively.

In the first part of this paper, Yau's estimates for positive L-harmonic functions and Li and Yau's gradient estimates for the positive solutions of a general parabolic heat equation on a complete Riemannian manifold are obtained by the use of Bakry and Emery's theory. In the second part we establish a heat kernel bound for a second-order differential operator which has a bounded and measurable drift, using Girsanov's formula.

A representation theory for the Hankel transformation Hv, defined for suitable f and for v > −1, by

on the spaces ℒμ, p defined by the norm

is developed. Using this, representation theories are developed for some related transformations.

For a smooth, simple closed curve α in the plane, the perpendicular bisector map P associates to each pair of distinct points (p, q) on α the perpendicular bisector of the chord joining p and q. To a pair (p, p), the map P associates the normal to α at p. The set of critical values of this map is the union of the dual of the symmetry set of α and the dual of the evolute. (The symmetry set is the locus of the centres of circles bitangent to α.) We study the mapP and use it to give a complete list of the transitions which take place on the dual of the symmetry set and the dual of the evolute, as α varies in a generic one-parameter family of plane curves.

We study the asymptotic behaviour as t → ∞ of the solution u = u(x, t) ≧ 0 to the quasilinear heat equation with absorption ut = (um)xx − f(u) posed for t > 0 in a half-line I = { 0 < x < ∞}. For definiteness, we take f(u) = up but the results generalise easily to more general power-like absorption terms f(u). The exponents satisfy m > 1 and p >m. We impose u = 0 on the lateral boundary {x = 0, t > 0}, and consider a non-negative, integrable and compactly supported function uo(x) as initial data. This problem is equivalent to solving the corresponding equation in the whole line with antisymmetric initial data, uo(−x) = −uo(x).

We give an explicit expression for the quasiconvex envelope of the Saint Venant–Kirchhoff stored energy function in terms of the singular values. This envelope is also the convex, polyconvex and rank 1 convex envelope of the Saint Venant–Kirchhoff stored energy function. Moreover, it coincides with the Saint Venant–Kirchhoff stored energy function itself on, and only on, the set of matrices whose singular values arranged in increasing order are located outside an ellipsoid. It vanishes on, and only on, the set of matrices whose singular values are less than 1. Consequently, a Saint Venant–Kirchhoff material can be compressed under zero external loading.

The paper discusses the asymptotic behaviour of weak solutions u(t, x), as t → ∞, to the boundary value problem for one-dimensional viscoelastic equations with singular memory. The changes of phase are admitted for the problem. One of our results is that ut(t, ·)⇀0 weakly in L2(0,1) as t → ∞.

The Weierstrass necessary condition for a multidimensional basic variational problem due to Hadamard is strengthened.

We show that for every finite set A and for every natural number n, there exists a natural number N such that every word of length N over the alphabet A has, for every permutation π of the numbers 1,…,n, a representation of the form Xw1 … wnzwπ(1) … wπ(n) Y, where X, Y are words and w1,…,wn, z are nonempty words over A.

It is shown that Hankel transforms of functions on certain weighted LP spaces satisfy Lipschitz and integral Lipschitz conditions. In particular, Fourier-cosine and Fourier-sine transforms satisfy such Lipschitz conditions on such spaces.

In this paper, we consider an n-dimensional semilinear equation of parabolic type with a discontinuous source term arising from combustion theory. We prove local existence for a classical solution having a ‘regular’ free boundary. In this regard, the free boundary is a surface through which the discontinuous source term exhibits a switch-like behaviour. We specify conditions under which this solution and its free boundary are global in time; moreover, we exhibit a special domain for which, for t tending to infinity, such a global-in-time solution converges, together with its free boundary, to the solution of the stationary problem and to its regular free boundary (which is proved to exist), respectively. We also prove uniqueness and continuous dependence theorems.

We classify completely integrable holonomic systems of first-order differential equations for one real-valued function by equivalence under the group of point transformations in the sense of Sophus Lie. In order to pursue the classification, we use the notion of one parameter Legendrian unfoldings which induces a special class of divergent diagrams of map germs which are called integral diagrams. Our normal forms are represented by integral diagrams.

We define a quantity called the reduced C* exponential rank rcel (A) of a C*-algebra A, which satisfies rcel (A) ≦ cel (A). We show that rcel (A) = ∞ whenever A has two distinct normalised traces which agree on K0(A), and we prove a partial converse. This gives some understanding of why cel (A) = π cer (A) for some C*-algebras A but not for others. We also characterise rcel (A) as the supremum of the rectifiable distances from unitaries in the identity component of the unitary group to the commutator subgroup of this component.

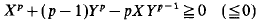
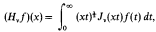
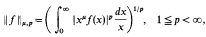
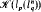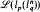Let 1 < p, q < ∞. It is shown for complex scalars that there are no nontrivial M-ideals in ℒ(Lp[0, 1]) if p ≠ 2, and is the only nontrivial M-ideal in .