We present new explicit solutions to some classes of quasilinear evolution equations arising in different applications, including equations of the Boussinesq type:

and quasilinear heat equations:

The method is based on construction of finite-dimensional linear functional subspaces which are invariant with respect to spatial operators having quadratic nonlinearities. The corresponding nonlinear evolution equations on invariant subspaces are shown to be equivalent to finite-dimensional dynamical systems. Examples of two-, three- and five- dimensional invariant subspaces are given. Some generalisations to N-dimensional quadratic operators are also considered.

Given an elliptic operator L on a bounded domain Ω ⊆ Rn, and a positive Radon measure μ on Ω, not charging polar sets, we discuss an explicit approximation procedure which leads to a sequence of domains Ωh ⊇ Ω with the following property: for every f ∈ H−1(Ω) the sequence uh of the solutions of the Dirichlet problems Luh = f in Ωh, uh = 0 on ∂Ωh, extended to 0 in Ω\Ωh, converges to the solution of the “relaxed Dirichlet problem” Lu + μu = f in Ω, u = 0 on ∂Ω.

If TRf(x) is the spherical partial sum of the Fourier transform of f and T*f(x) = SUPR > 0 | TRf(x)|, sufficient conditions are given on the non-negative weight function ω(x) which ensure that T* restricted to radial functionsis bounded on the Lorentz space Lp,s(Rn,ω) into Lp,q(Rn, ω) For power weights, these conditions are also necessary. The weight pairs (u,v) for which the generalised Stieltjes transform Sλ is bounded from LP,S(R+, v)into Lp,q(R+, u)are also characterised. These are an essential ingredient for the study of T*.

In the last few years, there has been considerable interest in the properties of orthogonal polynomials satisfying differential equations (DE) of order greater than two, their connection to singular boundary value problems, their generalizations, and their classification as solutions of second order DE (see for instance [2–8]). In this last interesting problem, some known facts about the classical orthogonal polynomials can be incorporated to connect these two sets of families and yield some nontrivial results in a very simple way. In this paper we only work with the nonclassical Jacobi type, Laguerre type and Legendre type polynomials, and we show how they can be connected with the classical Jacobi, Laguerre and Legendre polynomials, respectively; at the same time we obtain certain bounds for the zeros of the first ones by using a system of nonlinear equations satisfied by the zeros of any polynomial solution of a second order differential equation which, for the classical polynomials is known since Stieltjes and concerns the electrostatic interpretation of the zeros [10, Section 6.7; 9,1]. We also correct an expression for the second order differential equation of the Legendre type polynomials that circulates through the literature.

This paper is devoted to the study of the singular limit of the minimal solutions, as p → 1, of quasilinear Neumann problems involving p-Laplacian operators. It is established that the limit function is of bounded variation and is locally Höolder-continuous inside the domain.

Let φ:ℝ→ℝ be defined by φ(s) = |s|p−2s, with p > 1 a fixed number. We extend Sturm Comparison Theorem of the linear differential equation

to the nonlinear differential equation

by using the Wirtinger inequality. A Lyapunov inequality and some oscillation criteria of (E) are also given.

We prove that a Banach lattice X is reflexive if and only if X+ does not contain a closed normal cone with an unbounded closed dentable base.

As a generalisation of the well-known result of Perron and Frobenius, it was shown by Rothblum [13] and independently by Richman and Schneider [12] that every nonzero matrix with non-negative entries has a basis of the root space corresponding to the maximal eigenvalue, represented by root vectors with non-negative entries. Krein and Rutman [9] showed that a positive compact nonquasinilpotent operator on a Banach lattice has a positive eigenvector corresponding to its spectral radius. As an extension of both results, we give sufficient conditions on such an operator in order that its spectral subspace corresponding to its spectral radius has a basis made exclusively of positive root vectors.

We establish lower and upper bounds which are valid for the overall conductivity of twodimensional composites. They are based on a method which modifies the so-called translation method in a way which makes it effectively much more flexible. When specialised to composites of n > 2 isotropic phases, the new bounds are often strictly better than all the previously known ones. From the mathematical point of view, the improvement is due mainly to a new regularity result in p.d.e.s [2]. From the physical point of view the latter can be interpreted as a result bounding in a suitable sense the fluctuations of the ‘electric field’.

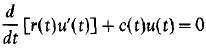
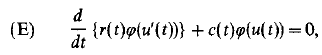
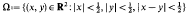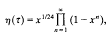
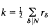Cardinal interpolation by integer translates of shifted three-directional box splines is studied. It is shown that, for arbitrary orders, k, l, m ∈ N of the directional vectors, this problem is correct if and only if the shift vector is taken from the hexagonal shift region (modulo translation with respect to the lattice Z2). This confirms a conjecture of S. D. Riemenschneider [9], and settles the problem studied in [5] for the special case k = l = m in full generality. The method of proof is from homotopy theory.

A kernel functor (equivalently, a left exact torsion preradical) is a left exact subfunctor of the identity on the category R-mod of left R-modules over a ring R with identity. A kernel functor is said to be idempotent if, in addition, σ satisfies σ(M / σ(M)) = 0 for every M ∊ R-mod. To every kernel functor / there corresponds a unique topologizing filter ℒσ = {I Ⅰ σ (R/I) = R/I} of left ideals and a unique class ℱσ = {M ∊ R-mod Ⅰ σ(M) = M} that is closed under homomorphic images, submodules, and direct sums. The idempotence of σ is characterized by either of the following additional conditions:

(1) if I ∊ ℒσ, K ⊆ I, and (K:x) = {r ∊ R ∣ rx ∊ K} ∊ ℒσ for each x ∊ I, then K ∊ ℒ or

(2) ℱσ is closed under extensions of one member of ℱσ by another member of ℱσ Idempotent kernel functors are important since they are the tool used to construct localization functors. For M∊ R-mod, let E(M) denote the injective hull of M. A kernel functor σ is called stable if Mℱ implies that E(M) ∊ ℱσ For more information about kernel functors, see [6], [7], [14], and [15].

Bass [1] proved that if R is a left perfect ring, then R contains no infinite sets of orthogonal idempotents and every nonzero left R-module has a maximal submodule, and asked if this property characterizes left perfect rings ([1], Remark (ii), p. 470). The fact that this is true for commutative rings was proved by Hamsher [12], and that this is not true in general was demonstrated by examples of Cozzens [7] and Koifman [14]. Hamsher's result for commutative rings has been extended to some noncommutative rings. Call a ring left duo if every left ideal is two-sided; Chandran [5] proved that Bass’ conjecture is true for left duo rings. Call a ring R weakly left duo if for every r ε R, there exists a natural number n(r) (depending on r) such that the principal left ideal Rrn(r) is two-sided. Recently, Xue [21] proved that Bass’ conjecture is still true for weakly left duo rings.

In a recent work, G. Anzellotti and the present authors introduced a notion of variation for functions defined over a rectifiable current. In this paper, we give a definition of a curvature varifold slightly different from that of Hutchinson (equivalent in the nonoriented case) and we study the variation properties, in the sense of [2], of the normal to a rectifiable current when the associated varifold is a curvature varifold.

The Dedekind η-function is defined by

where τ lies in the upper half plane ℋ = {tau;|Im(τ) > 0}, and x = e2πiτ. It is a modular form of weight ½ with a multiplier system. We define an η-product to be a function f (τ) of the form

where rδ ε ℤ. This is a modular form of weight with a multiplier system. The Fourier coefficients of η-products are related to many well-known number-theoretic functions, including partition functions and quadratic form representation numbers. They also arise from representations of the “monster” group [3] and the Mathieu group M24 [13]. The multiplicative structure of these Fourier coefficients has been extensively studied. Recent papers include [1], [4], [5] and [6]. Here we study the connections between the density of the non-zero Fourier coefficients of f(τ) and the representability of f(τ) as a linear combination of Hecke character forms (defined in Section 4 below). We first make the following definition.

In this paper, we provide sufficient conditions which guarantee the uniform stability as well as asymptotic stability of the positive equilibrium for a food limited population model with time delay.

Let f be an odd, C2 function on [− 1, 1], which vanishes at ± 1, and such that f′(O) < 0, f′ (±1) > 0 and u ↦ f(u)/u is increasing. Dang, Fife and Peletier [5] showed that there is a unique solution u with values in [−1, 1] of

which has the same sign as xy. The linearised operator around u is B defined by

It is proved here that the spectrum of B contains at least one negative eigenvalue, that all eigenfunctions corresponding to negative eigenvalues have the symmetries of the square, and that for Allen–Cahn's nonlinearity (f(u) = 2u3 − 2u), there is exactly one negative eigenvalue.

The paper provides an example of an integral functional in more than two dimensions, with a symmetric and positively defined quadratic integrand q, exhibiting the Lavrentieff phenomenon on a ball B and on a linear boundary datum u0, i.e. for which

The example is also utilised to discuss nonidentity between some relaxation procedures for a quadratic integral functional and to provide a weighted Sobolev space in the Hilbert case in which smooth functions are not dense.

A plot of the bifurcation diagram for a two-component reaction-diffusion equation with no-flux boundary conditions reveals an intricate web of competing stable and unstable states. By studying the one-dimensional Sel'kov model, we show how a mixture of local, global and numerical analysis can make sense of several aspects of this complex picture. The local bifurcation analysis, via the power of singularity theory, gives us a framework to work in. We can then fill in the details with numerical calculations, with the global analytic results fixing the outline of the solution set. Throughout, we discuss to what extent our results can be applied to other models.