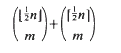Refine search
Actions for selected content:
25814 results in Abstract analysis
Properties (V) and (u) are not three-space properties
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 297-299
- Print publication:
- September 1994
-
- Article
-
- You have access
- Export citation
On dilation equations and the Hölder continuity of the de Rham functions
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 309-311
- Print publication:
- September 1994
-
- Article
-
- You have access
- Export citation
Capitulation in unramified quadratic extensions of real quadratic number fields
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 385-392
- Print publication:
- September 1994
-
- Article
-
- You have access
- Export citation
Local spectral theory and spectral inclusions
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 331-343
- Print publication:
- September 1994
-
- Article
-
- You have access
- Export citation
GMJ volume 36 issue 3 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- September 1994
-
- Article
-
- You have access
- Export citation
GMJ volume 36 issue 3 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f9
- Print publication:
- September 1994
-
- Article
-
- You have access
- Export citation
Coranks of a quasi-projective module and its endomorphism ring
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 381-383
- Print publication:
- September 1994
-
- Article
-
- You have access
- Export citation
On quasi-permutation representations of finite groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 301-308
- Print publication:
- September 1994
-
- Article
-
- You have access
- Export citation
Defining-relations for Hurwitz groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 363-370
- Print publication:
- September 1994
-
- Article
-
- You have access
- Export citation
On the Arens semi-regularity of weighted group algebras
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 269-275
- Print publication:
- September 1994
-
- Article
-
- You have access
- Export citation
Pure-semisimplicity is preserved under elementary equivalence
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 345-346
- Print publication:
- September 1994
-
- Article
-
- You have access
- Export citation
MTK volume 41 issue 1 Cover and Front matter
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
- Print publication:
- June 1994
-
- Article
-
- You have access
- Export citation
Detecting exotic structures via the Pontrjagin-Thom construction
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 145-148
- Print publication:
- June 1994
-
- Article
- Export citation
The number of zero sums modulo m in a sequence of length n
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 149-163
- Print publication:
- June 1994
-
- Article
- Export citation
Borel and analytic sets in Banach spaces
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 133-140
- Print publication:
- June 1994
-
- Article
- Export citation
On the nonlinear growth of single three-dimensional disturbances in boundary layers
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-39
- Print publication:
- June 1994
-
- Article
- Export citation
Dimension prints of fractal sets
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 68-94
- Print publication:
- June 1994
-
- Article
- Export citation
L. Aizenberg. Carleman's Formula in Complex Analysis. Kluwer. 1993, 300 pp., £90. - B. Amberg, S. Franciosi and F. de Giovanni. Products of Groups. Clarendon Press. 1992, 218 pp., £45. - Michael Artin. Algebra. Birkhäuser. 1993, 705 pp., Swiss Fr.78. - L. W. Baggett. Functional Analysis—A Primer. Marcel Dekker. 1992, 288 pp., $49.75. - Y. Bahturin. Basic Structures of Modern Algebra. Kluwer Academic. 1993, 419 pp., £122·50. - D. Bainov and P. Simeonov. Impulsive Differential Equations: Periodic Solutions and Applications. Longman. 1993, 228 pp., £38. - D. Daners and P. K. Medina. Abstract evolution equations, periodic problems and applications. Longman. 1992, 249 pp., £28. - R. Deville, G. Godefroy and V. Zizler. Smoothness and Renormings in Banach Space. Longman. 1993, 375 pp., £52. - T. Dracos and A. Tsinober. New Approaches and Concepts in Turbulence. Birkhäuser. 1993, 426 pp., £56. - I. Gohberg and N. Krupnik. One-Dimensional Linear Singular Integral Equations.. Birkhäuser. 1992, 267 pp., Swiss Fr.128. - L. S. Grinblat. On sets not belonging to algebras of subsets. Amer. Math.Soc. 1992, 111 pp., £18. - S. Guerre-Delabrière. Classical Sequences in Banach Spaces. Marcel Dekker. 1992, 232 pp., $99.75. - C. Hog-Angeloni, W. Metzler and A. J. Sieradski. Two dimensional homotopy and combinatorial group theory. Cambridge University Press. 1993, 412 pp., £25. - I. T. Kiguradze and T. A. Chanturia. Asymptotic Properties of Solutions of Nonautonomous Ordinary Differential Equations. Kluwer. 1993, 331 pp., £92·50. - L. C. Kinsey. Topology of Surfaces. Springer. 1993, 262 pp., DM 68. - S. H. Kulkarni and B. V. Limaye. Real Function Algebras. Marcel Dekker. 1992, 200 pp., $99.75. - D. B. Meli. Equivalence and Priority: Newton versus Leibniz, including Leibniz's unpublished Manuscripts on the Principia. Clarendon Press. 1993, 318 pp., with 60 Figures and 7 plates, £55. - S. Martin. Schur Algebras and Representation Theory. Cambridge Tracts in Mathematics No. 112. Cambridge University Press. 1993, 232 pp., £30. - A. L. Onishchik. Topology of Transitive Transformation Groups. J. A. Barth. 1994, 300 pp., DM 160. - P. G. Saffman. Vortex Dynamics. Cambridge University Press. 1993, 311 pp., £35. - S. K. Sehgal. Units in Integral Group Rings. Longman. 1993, 356 pp., £57. - H. M. Srivastava and R. G. Buschman. Theory and Applications of Convolution Integral Equations. Kluwer. 1992, 240 pp., £56. - I. Tamura. Topology of Foliations: An Introduction. Amer. Math. Soc. 1992, 190 pp., £61. - H. Triebel. Theory of Function Spaces II. Birkhäuser. 1992, 370 pp., Swiss Fr. 158.
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 215-220
- Print publication:
- June 1994
-
- Article
- Export citation
A regular endomorphism of a graph and its inverses
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 189-198
- Print publication:
- June 1994
-
- Article
- Export citation
On the relation type of large powers of an ideal
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 209-214
- Print publication:
- June 1994
-
- Article
- Export citation
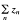 in
in 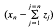 is weakly null. It is said that
is weakly null. It is said that 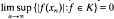 for every wuC series
for every wuC series 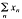 in
in 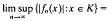 0 for every wuC series
0 for every wuC series 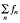 in
in 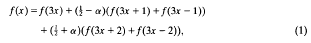

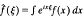 is the Fourier transform of
is the Fourier transform of 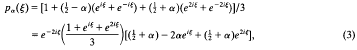

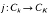
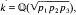 with distinct primes
with distinct primes