Refine search
Actions for selected content:
25814 results in Abstract analysis
Contents
-
- Book:
- Invariant Potential Theory in the Unit Ball of Cn
- Published online:
- 15 December 2009
- Print publication:
- 12 May 1994, pp vii-viii
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Invariant Potential Theory in the Unit Ball of Cn
- Published online:
- 15 December 2009
- Print publication:
- 12 May 1994, pp i-vi
-
- Chapter
- Export citation
References
-
- Book:
- Invariant Potential Theory in the Unit Ball of Cn
- Published online:
- 15 December 2009
- Print publication:
- 12 May 1994, pp 164-170
-
- Chapter
- Export citation
Polycyclic group rings and unique factorisation rings
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 135-144
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
Classification of tensor product immersions which are of 1-type
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 255-264
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
On 𝓕-subnormal subgroups and Frattini-like subgroups of a finite group
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 241-247
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
The kernel and trace operators for ideal extensions of regular semigroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 219-231
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
On reducible braids and composite braids
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 197-199
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
GMJ volume 36 issue 2 Cover and Front matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
Linearization of holomorphic mappings on fully nuclear spaces with a basis
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 201-208
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
Symmetries of surfaces: an extension of Kulkarni's theorem
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 173-184
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
Extension of completely bounded A-B bimodule maps†
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 145-155
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
Fitting classes of certain metanilpotent groups
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 185-195
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
Remarks on the range of a vector measure
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 157-161
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
Finite metacyclic groups acting on bordered surfaces
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 233-240
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
A weaker condition for normality
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 249-253
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
Associate subgroups of orthodox semigroups
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 163-171
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
The structure of discontinuous homomorphisms from non-commutative C*-algebras
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. 209-218
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
GMJ volume 36 issue 2 Cover and Back matter
-
- Journal:
- Glasgow Mathematical Journal / Volume 36 / Issue 2 / May 1994
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
- Print publication:
- May 1994
-
- Article
-
- You have access
- Export citation
3 - Commutative Algebras and Functional Calculus
-
- Book:
- Banach Algebras and the General Theory of *-Algebras
- Published online:
- 05 May 2013
- Print publication:
- 25 March 1994, pp 301-436
-
- Chapter
- Export citation
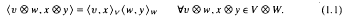
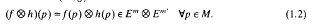
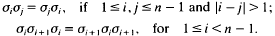
 (
(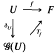
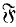 (
(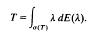
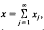 then this sum must converge unconditionally.
then this sum must converge unconditionally.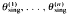 :
: 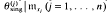
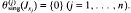 is a homomorphism, and
is a homomorphism, and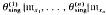
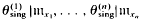 to map into rad(
to map into rad(