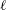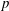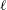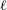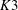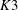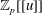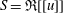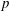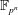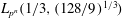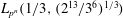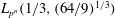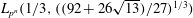Refine search
Actions for selected content:
2567 results in Computational Science
A sieve algorithm based on overlattices
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 49-70
-
- Article
-
- You have access
- Export citation
Minimal models for
 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}6$-coverings of elliptic curves
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}6$-coverings of elliptic curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 112-127
-
- Article
-
- You have access
- Export citation
Computing Hasse–Witt matrices of hyperelliptic curves in average polynomial time
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 257-273
-
- Article
-
- You have access
- Export citation
Computation of Mordell–Weil bases for ordinary elliptic curves in characteristic two
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 1-13
-
- Article
-
- You have access
- Export citation
Computing Galois representations of modular abelian surfaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 36-48
-
- Article
-
- You have access
- Export citation
Hyper-and-elliptic-curve cryptography
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 181-202
-
- Article
-
- You have access
- Export citation
Subexponential class group and unit group computation in large degree number fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 385-403
-
- Article
-
- You have access
- Export citation
Nonvanishing of twists of
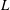 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$-functions attached to Hilbert modular forms
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$-functions attached to Hilbert modular forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 330-348
-
- Article
-
- You have access
- Export citation
On the quaternion
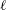 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\ell $-isogeny path problem
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\ell $-isogeny path problem
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 418-432
-
- Article
-
- You have access
- Export citation
Examples of
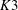 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K3$ surfaces with real multiplication
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K3$ surfaces with real multiplication
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 14-35
-
- Article
-
- You have access
- Export citation
Parametrizing the moduli space of curves and applications to smooth plane quartics over finite fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 128-147
-
- Article
-
- You have access
- Export citation
Linear algebra over
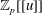 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}_p[[u]]$ and related rings
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}_p[[u]]$ and related rings
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 302-344
-
- Article
-
- You have access
- Export citation
Computing in quotients of rings of integers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 349-365
-
- Article
-
- You have access
- Export citation
The multiple number field sieve for medium- and high-characteristic finite fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 230-246
-
- Article
-
- You have access
- Export citation
Appendix A - Installing a Python environment
-
- Book:
- Python for Scientists
- Published online:
- 05 August 2014
- Print publication:
- 10 July 2014, pp 205-209
-
- Chapter
- Export citation
Index
-
- Book:
- Python for Scientists
- Published online:
- 05 August 2014
- Print publication:
- 10 July 2014, pp 218-220
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Python for Scientists
- Published online:
- 05 August 2014
- Print publication:
- 10 July 2014, pp 1-10
-
- Chapter
- Export citation
References
-
- Book:
- Python for Scientists
- Published online:
- 05 August 2014
- Print publication:
- 10 July 2014, pp 216-217
-
- Chapter
- Export citation
9 - Case study: multigrid
-
- Book:
- Python for Scientists
- Published online:
- 05 August 2014
- Print publication:
- 10 July 2014, pp 184-204
-
- Chapter
- Export citation
2 - Getting started with IPython
-
- Book:
- Python for Scientists
- Published online:
- 05 August 2014
- Print publication:
- 10 July 2014, pp 11-19
-
- Chapter
- Export citation