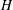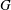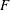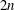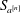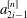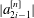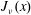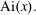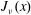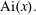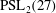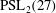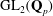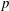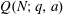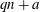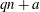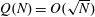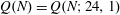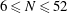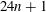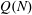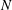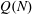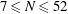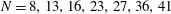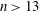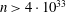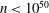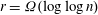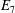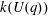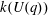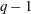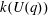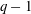Refine search
Actions for selected content:
2567 results in Computational Science
Computation of Galois groups of rational polynomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 141-158
-
- Article
-
- You have access
- Export citation
A note on magnitude bounds for the mask coefficients of the interpolatory Dubuc–Deslauriers subdivision scheme
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 226-232
-
- Article
-
- You have access
- Export citation
A note on uniform approximation of functions having a double pole
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 233-244
-
- Article
-
- You have access
- Export citation
Approximations for the Bessel and Airy functions with an explicit error term
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 209-225
-
- Article
-
- You have access
- Export citation
Minimal genus and fibering of canonical surfaces via disk decomposition
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 77-108
-
- Article
-
- You have access
- Export citation
Classification of subgroups isomorphic to
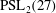 $\mathrm{PSL}_2(27)$ in the Monster
$\mathrm{PSL}_2(27)$ in the Monster
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 33-46
-
- Article
-
- You have access
- Export citation
Computing fundamental domains for the Bruhat–Tits tree for
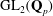 ${\rm GL}_2(\mathbf{Q}_p)$ ,
${\rm GL}_2(\mathbf{Q}_p)$ , 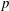 $p$ -adic automorphic forms, and the canonical embedding of Shimura curves
$p$ -adic automorphic forms, and the canonical embedding of Shimura curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 1-23
-
- Article
-
- You have access
- Export citation
On a conjecture of Rudin on squares in arithmetic progressions
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 58-76
-
- Article
-
- You have access
- Export citation
Wieferich pairs and Barker sequences, II
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 24-32
-
- Article
-
- You have access
- Export citation
Deterministic polynomial factoring and association schemes
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 123-140
-
- Article
-
- You have access
- Export citation
Calculating conjugacy classes in Sylow
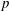 $p$ -subgroups of finite Chevalley groups of rank six and seven
$p$ -subgroups of finite Chevalley groups of rank six and seven
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 109-122
-
- Article
-
- You have access
- Export citation
Bounds for zeros of Meixner and Kravchuk polynomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 47-57
-
- Article
-
- You have access
- Export citation
7 - Statistical analysis of mathematical models
-
- Book:
- Mathematical Modeling in Chemical Engineering
- Published online:
- 05 June 2014
- Print publication:
- 20 March 2014, pp 121-167
-
- Chapter
- Export citation
5 - Strategies for simplifying mathematical models
-
- Book:
- Mathematical Modeling in Chemical Engineering
- Published online:
- 05 June 2014
- Print publication:
- 20 March 2014, pp 53-80
-
- Chapter
- Export citation
6 - Numerical methods
-
- Book:
- Mathematical Modeling in Chemical Engineering
- Published online:
- 05 June 2014
- Print publication:
- 20 March 2014, pp 81-120
-
- Chapter
- Export citation
3 - Model formulation
-
- Book:
- Mathematical Modeling in Chemical Engineering
- Published online:
- 05 June 2014
- Print publication:
- 20 March 2014, pp 20-39
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Mathematical Modeling in Chemical Engineering
- Published online:
- 05 June 2014
- Print publication:
- 20 March 2014, pp i-iv
-
- Chapter
- Export citation
Appendix A - Microscopic transport equations
-
- Book:
- Mathematical Modeling in Chemical Engineering
- Published online:
- 05 June 2014
- Print publication:
- 20 March 2014, pp 168-169
-
- Chapter
- Export citation
4 - Empirical model building
-
- Book:
- Mathematical Modeling in Chemical Engineering
- Published online:
- 05 June 2014
- Print publication:
- 20 March 2014, pp 40-52
-
- Chapter
- Export citation
Contents
-
- Book:
- Mathematical Modeling in Chemical Engineering
- Published online:
- 05 June 2014
- Print publication:
- 20 March 2014, pp v-viii
-
- Chapter
- Export citation