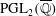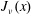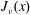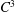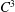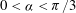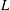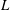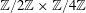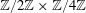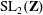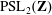Refine search
Actions for selected content:
2567 results in Computational Science
Appendix B - Fortran77 subroutines for pseudospectral methods
-
- Book:
- Python for Scientists
- Published online:
- 05 August 2014
- Print publication:
- 10 July 2014, pp 210-215
-
- Chapter
- Export citation
6 - Three-dimensional graphics
-
- Book:
- Python for Scientists
- Published online:
- 05 August 2014
- Print publication:
- 10 July 2014, pp 107-121
-
- Chapter
- Export citation
7 - Ordinary differential equations
-
- Book:
- Python for Scientists
- Published online:
- 05 August 2014
- Print publication:
- 10 July 2014, pp 122-162
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Python for Scientists
- Published online:
- 05 August 2014
- Print publication:
- 10 July 2014, pp i-iv
-
- Chapter
- Export citation
8 - Partial differential equations: a pseudospectral approach
-
- Book:
- Python for Scientists
- Published online:
- 05 August 2014
- Print publication:
- 10 July 2014, pp 163-183
-
- Chapter
- Export citation
Preface
-
- Book:
- Python for Scientists
- Published online:
- 05 August 2014
- Print publication:
- 10 July 2014, pp xi-xii
-
- Chapter
- Export citation
3 - A short Python tutorial
-
- Book:
- Python for Scientists
- Published online:
- 05 August 2014
- Print publication:
- 10 July 2014, pp 20-51
-
- Chapter
- Export citation
4 - Numpy
-
- Book:
- Python for Scientists
- Published online:
- 05 August 2014
- Print publication:
- 10 July 2014, pp 52-78
-
- Chapter
- Export citation
Contents
-
- Book:
- Python for Scientists
- Published online:
- 05 August 2014
- Print publication:
- 10 July 2014, pp v-x
-
- Chapter
- Export citation
5 - Two-dimensional graphics
-
- Book:
- Python for Scientists
- Published online:
- 05 August 2014
- Print publication:
- 10 July 2014, pp 79-106
-
- Chapter
- Export citation
A census of quadratic post-critically finite rational functions defined over
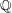 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Q}$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Q}$
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 July 2014, pp. 314-329
-
- Article
-
- You have access
- Export citation

From Error-Correcting Codes through Sphere Packings to Simple Groups
-
- Published by:
- Mathematical Association of America
- Published online:
- 05 June 2014
- Print publication:
- 01 June 1983
-
- Book
- Export citation

Mathematical Modeling in Chemical Engineering
-
- Published online:
- 05 June 2014
- Print publication:
- 20 March 2014
On the Bessel function
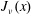 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}J_\nu (x)$ in the transition region
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}J_\nu (x)$ in the transition region
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 June 2014, pp. 273-281
-
- Article
-
- You have access
- Export citation
A symmetric
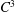 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^{3}$ non-stationary subdivision scheme
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^{3}$ non-stationary subdivision scheme
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 June 2014, pp. 259-272
-
- Article
-
- You have access
- Export citation
Evaluating
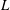 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$ -functions with few known coefficients
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$ -functions with few known coefficients
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 June 2014, pp. 245-258
-
- Article
-
- You have access
- Export citation
High-rank elliptic curves with torsion
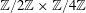 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/4\mathbb{Z}$ induced by Diophantine triples
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/4\mathbb{Z}$ induced by Diophantine triples
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 June 2014, pp. 282-288
-
- Article
-
- You have access
- Export citation
On the beta expansion of Salem numbers of degree 8
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 June 2014, pp. 289-301
-
- Article
-
- You have access
- Export citation
Congruence testing for odd subgroups of the modular group
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 206-208
-
- Article
-
- You have access
- Export citation
Rational functions with maximal radius of absolute monotonicity
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 159-205
-
- Article
-
- You have access
- Export citation