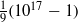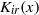Refine search
Actions for selected content:
2584 results in Computational Science
Chapter 8 - Solution of Hyperbolic PDEs: Signal and Error Propagation
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp 130-149
-
- Chapter
- Export citation
Chapter 9 - Curvilinear Coordinate and Grid Generation
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp 150-195
-
- Chapter
- Export citation
Václav Šimerka: quadratic forms and factorization
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 May 2013, pp. 118-129
-
- Article
-
- You have access
- Export citation
Minimal solvable nonic fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 May 2013, pp. 130-138
-
- Article
-
- You have access
- Export citation
Bounds and algorithms for the
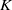 $K$ -Bessel function of imaginary order
$K$ -Bessel function of imaginary order
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 10 April 2013, pp. 78-108
-
- Article
-
- You have access
- Export citation
On the continuity of multivariate Lagrange interpolation at natural lattices
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 10 April 2013, pp. 45-60
-
- Article
-
- You have access
- Export citation
Complex B-splines and Hurwitz zeta functions
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 10 April 2013, pp. 61-77
-
- Article
-
- You have access
- Export citation
Computing zeta functions of nondegenerate hypersurfaces with few monomials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 14 February 2013, pp. 9-44
-
- Article
-
- You have access
- Export citation
A comprehensive perturbation theorem for estimating magnitudes of roots of polynomials
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 14 February 2013, pp. 1-8
-
- Article
-
- You have access
- Export citation
References
-
- Book:
- Generalized Vectorization, Cross-Products, and Matrix Calculus
- Published online:
- 05 February 2013
- Print publication:
- 11 February 2013, pp 257-258
-
- Chapter
- Export citation
Two - Zero-One Matrices
-
- Book:
- Generalized Vectorization, Cross-Products, and Matrix Calculus
- Published online:
- 05 February 2013
- Print publication:
- 11 February 2013, pp 28-88
-
- Chapter
- Export citation
Three - Elimination and Duplication Matrices
-
- Book:
- Generalized Vectorization, Cross-Products, and Matrix Calculus
- Published online:
- 05 February 2013
- Print publication:
- 11 February 2013, pp 89-133
-
- Chapter
- Export citation
Generalized Vectorization, Cross-Products, and Matrix Calculus - Title page
-
-
- Book:
- Generalized Vectorization, Cross-Products, and Matrix Calculus
- Published online:
- 05 February 2013
- Print publication:
- 11 February 2013, pp iii-iii
-
- Chapter
- Export citation
Symbols and Operators Used in this Book
-
- Book:
- Generalized Vectorization, Cross-Products, and Matrix Calculus
- Published online:
- 05 February 2013
- Print publication:
- 11 February 2013, pp 255-256
-
- Chapter
- Export citation
Index
-
- Book:
- Generalized Vectorization, Cross-Products, and Matrix Calculus
- Published online:
- 05 February 2013
- Print publication:
- 11 February 2013, pp 259-267
-
- Chapter
- Export citation
One - Mathematical Prerequisites
-
- Book:
- Generalized Vectorization, Cross-Products, and Matrix Calculus
- Published online:
- 05 February 2013
- Print publication:
- 11 February 2013, pp 1-27
-
- Chapter
- Export citation
Six - Applications
-
- Book:
- Generalized Vectorization, Cross-Products, and Matrix Calculus
- Published online:
- 05 February 2013
- Print publication:
- 11 February 2013, pp 214-254
-
- Chapter
- Export citation
Generalized Vectorization, Cross-Products, and Matrix Calculus - Half title page
-
- Book:
- Generalized Vectorization, Cross-Products, and Matrix Calculus
- Published online:
- 05 February 2013
- Print publication:
- 11 February 2013, pp i-ii
-
- Chapter
- Export citation
Contents
-
- Book:
- Generalized Vectorization, Cross-Products, and Matrix Calculus
- Published online:
- 05 February 2013
- Print publication:
- 11 February 2013, pp v-viii
-
- Chapter
- Export citation
Four - Matrix Calculus
-
- Book:
- Generalized Vectorization, Cross-Products, and Matrix Calculus
- Published online:
- 05 February 2013
- Print publication:
- 11 February 2013, pp 134-163
-
- Chapter
- Export citation