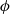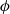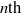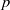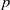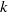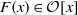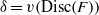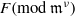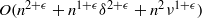Refine search
Actions for selected content:
2567 results in Computational Science
Explicit application of Waldspurger’s theorem
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 216-245
-
- Article
-
- You have access
- Export citation
Computing level one Hecke eigensystems (mod
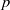 $p$ )
$p$ )
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 246-270
-
- Article
-
- You have access
- Export citation
Modular subgroups, dessins d’enfants and elliptic K3 surfaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 271-318
-
- Article
-
- You have access
- Export citation
Complexity of OM factorizations of polynomials over local fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 June 2013, pp. 139-171
-
- Article
-
- You have access
- Export citation
Frontmatter
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp i-iv
-
- Chapter
- Export citation
Contents
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp v-xii
-
- Chapter
- Export citation
Chapter 7 - Solution Methods for Elliptic Partial Differential Equations
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp 106-129
-
- Chapter
- Export citation
Chapter 11 - Higher Accuracy Methods
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp 256-340
-
- Chapter
- Export citation
Chapter 14 - Recent Developments in Discrete Finite Difference Computing
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp 442-534
-
- Chapter
- Export citation
Chapter 2 - Governing Equations in Fluid Mechanics
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp 8-30
-
- Chapter
- Export citation
Chapter 6 - Solution Methods for Parabolic Partial Differential Equations
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp 92-105
-
- Chapter
- Export citation
References
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp 546-562
-
- Chapter
- Export citation
Preface
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp xvii-xix
-
- Chapter
- Export citation
Chapter 10 - Spectral Analysis of Numerical Schemes and Aliasing Error
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp 196-255
-
- Chapter
- Export citation
Chapter 4 - Waves and Space–Time Dependence in Computing
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp 38-70
-
- Chapter
- Export citation
Chapter 13 - Solution of Navier–Stokes Equation
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp 405-441
-
- Chapter
- Export citation
Chapter 12 - Introduction to Finite Volume and Finite Element Methods
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp 341-404
-
- Chapter
- Export citation
Chapter 3 - Classification of Quasi-Linear Partial Differential Equations
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp 31-37
-
- Chapter
- Export citation
Exercises
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp 535-545
-
- Chapter
- Export citation
Foreward
-
- Book:
- High Accuracy Computing Methods
- Published online:
- 05 January 2014
- Print publication:
- 16 May 2013, pp xiii-xvi
-
- Chapter
- Export citation